题目内容
8.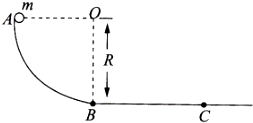 AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨相切,如图所示.一可视为质点的小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求:
AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨相切,如图所示.一可视为质点的小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求:(1)小球下滑到B点时速度的大小;
(2)小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力FB、FC各是多大?
分析 根据机械能守恒定律求出小球运动到B点的速度;根据牛顿第二定律求出B点的支持力大小,在C点支持力大小等于重力的大小
解答 解:(1)小球从A到B的运动过程中,机械能守恒,选BC所在水平面为参考平面,则:$mgR=\frac{1}{2}m{v}_{B}^{2}$ ①
则小球运动到B点时的速度为:${v}_{B}=\sqrt{2gR}$
(2)根据牛顿运动定律,小球在B点时,有:N-mg=m$\frac{{v}_{B}^{2}}{R}$,②
解①②得:NB=3mg
在C点:Nc=mg.
答:(1)小球运动到B点时的速度为$\sqrt{2gR}$.
(2)小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力NB、NC各是3mg、mg.
点评 本题考查了机械能守恒定律的基本运用,以及掌握圆周运动靠径向的合力提供向心力,通过牛顿第二定律求解支持力的大小

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.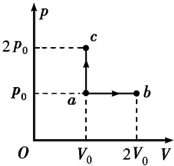 如图,一定质量的理想气体,由状态a经过ab过程到达状态b或者经过ac过程到达状态c.设气体在状态b和状态c的温度分别为Tb和Tc,在过程ab和ac中吸收的热量分别为Qab和Qac,则( )
如图,一定质量的理想气体,由状态a经过ab过程到达状态b或者经过ac过程到达状态c.设气体在状态b和状态c的温度分别为Tb和Tc,在过程ab和ac中吸收的热量分别为Qab和Qac,则( )
 如图,一定质量的理想气体,由状态a经过ab过程到达状态b或者经过ac过程到达状态c.设气体在状态b和状态c的温度分别为Tb和Tc,在过程ab和ac中吸收的热量分别为Qab和Qac,则( )
如图,一定质量的理想气体,由状态a经过ab过程到达状态b或者经过ac过程到达状态c.设气体在状态b和状态c的温度分别为Tb和Tc,在过程ab和ac中吸收的热量分别为Qab和Qac,则( )| A. | Tb>Tc,Qab>Qac | B. | Tb>Tc,Qab<Qac | C. | Tb=Tc,Qab>Qac | D. | Tb=Tc,Qab<Qac |
19.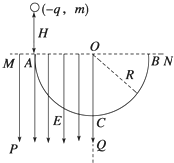 如图所示,ACB为光滑固定的半圆形轨道,轨道半径为R,A、B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$.一个质量为m,电荷量为-q的带电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.小球运动过程中电量不变,不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )
如图所示,ACB为光滑固定的半圆形轨道,轨道半径为R,A、B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$.一个质量为m,电荷量为-q的带电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.小球运动过程中电量不变,不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )
 如图所示,ACB为光滑固定的半圆形轨道,轨道半径为R,A、B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$.一个质量为m,电荷量为-q的带电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.小球运动过程中电量不变,不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )
如图所示,ACB为光滑固定的半圆形轨道,轨道半径为R,A、B为圆水平直径的两个端点,AC为$\frac{1}{4}$圆弧,MPQO为有界的竖直向下的匀强电场,电场强度的大小E=$\frac{2mg}{q}$.一个质量为m,电荷量为-q的带电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.小球运动过程中电量不变,不计空气阻力及一切能量损失,已知重力加速度为g,关于带电小球的运动情况,下列说法正确的是( )| A. | 若H=R,则小球到达C点的速度为零 | B. | 若H=2R,则小球到达B点的速度为零 | ||
| C. | 若H=3R,则小球到达C点的速度$\sqrt{2gR}$ | D. | 若 H=4R,则小球到达B点的速度$\sqrt{2gR}$ |
13.关于粒子的说法,正确的是( )
| A. | 组成阴极射线的带电粒子是α粒子 | |
| B. | 卢瑟福在利用α粒子轰击氮原子核的实验中发现了质子 | |
| C. | 发生光电效应时,从金属表面逸出的粒子是光子 | |
| D. | 查德威克在利用α粒子轰击铍原子核的实验中发现了电子 |
20. 如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )
如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )
 如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )
如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )| A. | M点处放置的是正电荷 | |
| B. | d点的电势高于f点的电势 | |
| C. | d点的场强与f点的场强相同 | |
| D. | 将带正电的试探电荷沿直线由d点移动到f点,电势能先增大后减小 |
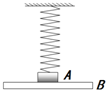 轻质弹簧上端固定,下端连接质量m=3kg的物块A,物块A放在平台B上,通过平台B可以控制A的运动,如图所示.初始时A、B静止,弹簧处于原长.已知弹簧的劲度系数k=200N/m,g=10m/s2.(计算结果保留两位有效数字)
轻质弹簧上端固定,下端连接质量m=3kg的物块A,物块A放在平台B上,通过平台B可以控制A的运动,如图所示.初始时A、B静止,弹簧处于原长.已知弹簧的劲度系数k=200N/m,g=10m/s2.(计算结果保留两位有效数字)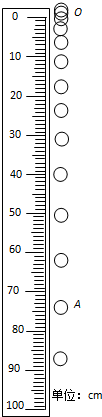 为验证小球在自由下落过程中机械能守恒,某实验小组进行了如下操作:
为验证小球在自由下落过程中机械能守恒,某实验小组进行了如下操作: