Question

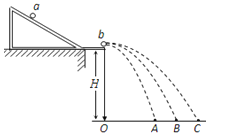
【题目】如图，水平平台上有一轻弹簧，左端固定在A点，自然状态时其右端位于B点，平台AB段光滑，BC段长x＝1m，与滑块间的摩擦因数为μ1＝0.25．平台右端与水平传送带相接于C点，传送带的运行速度v＝7m/s，长为L＝3m，传送带右端D点与一光滑斜面衔接，斜面DE长度S＝0.5m，另有一固定竖直放置的光滑圆弧形轨道刚好在E点与斜面相切，圆弧形轨道半径R＝1m，θ＝37°．今将一质量m＝2kg的滑块向左压缩轻弹簧到最短，此时弹簧的弹性势能为EP＝30J，然后突然释放，当滑块滑到传送带右端D点时，恰好与传送带速度相同。设经过D点的拐角处无机械能损失且滑块能沿斜面下滑。重力加速度g＝10m/s2，sin53°＝0.8，cos53°＝0.6，不计空气阻力。试求：

（1）滑块到达C点的速度vC＝？

（2）滑块与传送带间的摩擦因数μ2及经过传送带过程系统因摩擦力增加的内能；

（3）若传送带的运行速度可调，要使滑块不脱离圆弧形轨道，求传送带的速度范围.

Answer 1

【答案】（1）5m/s（2）μ2=0.4，E内＝24J（3）0≤v传m/s或v传≥2m/s

【解析】

（1）以滑块为研究对象，从释放到C点的过程，由动能定理得：

代入数据得：vC＝5m/s

（2）滑块从C点到D点一直加速，到D点恰好与传送带同速，由动能定理得：

代入数据解得：μ2＝0.4

经过传送带过程系统因摩擦力增加的内能为

E内＝μ2mg△x

其中

代入数据解得E内＝24J

（3）斜面高度为：

h＝ssinθ＝0.3m

（Ⅰ）设滑块在D点的速度为vD1时，恰好过圆弧最高点，由牛顿第二定律得：

滑块从D点到G点的过程，由动能定理得：

代入数据解得：

（Ⅱ）设滑块在D点的速度为vD2时，恰好到圆弧处速度为零，此过程由动能定理得：

代入数据解得：

若滑块在传送带上一直减速至D点恰好同速，则由动能定理得：

代入数据解得：v传1＝1m/s，所以

若滑块在传送带上一直加速至D点恰好同速，由题目已知v传2＝7m/s

所以.