题目内容
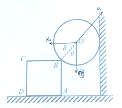
【题目】在竖直墙壁的左侧水平地面上,放置一个边长为a、质量为M的正方体ABCD,在墙壁和正方体之间放置一半径为R、质量为m的光滑球,正方体和球均保持静止,如图所示。球的球心为O,OB与竖直方向的夹角为![]() ,正方体的边长a>R,正方体与水平地面的动摩擦因数为
,正方体的边长a>R,正方体与水平地面的动摩擦因数为![]() 。(g已知,并取最大静摩擦力等于滑动摩擦力)求:
。(g已知,并取最大静摩擦力等于滑动摩擦力)求:

(1)正方体和墙壁对球的支持力N1、N2分别是多大?
(2)若![]() =45°,保持球的半径不变,只增大球的质量,为了不让正方体出现滑动,则球质量的最大值为多少?(tan45°=1)。
=45°,保持球的半径不变,只增大球的质量,为了不让正方体出现滑动,则球质量的最大值为多少?(tan45°=1)。
(3)改变正方体到墙壁之间的距离,球和正方体都处于静止状态,且球没有掉落地面。若不让正方体出现滑动,讨论以下情况:
a. 若球的质量m=![]() M,则正方体的右侧面AB到墙壁的最大距离是多少?
M,则正方体的右侧面AB到墙壁的最大距离是多少?
b. 当正方体的右侧面AB到墙壁的距离小于某个值时,则无论球的质量是多少,正方体都不会滑动,则这个距离的值是多少?
【答案】(1)N1=mg/cos![]() ,N2=mgtan
,N2=mgtan![]() ;(2)m<
;(2)m<![]() ;(3)a.
;(3)a. ![]() R;b.
R;b. ![]() R。
R。
【解析】
(1)以球为研究对象,受力如图:
小球受力平衡:N1cosθ=mg,N1=![]()
N2=mgtanθ;
(2)以正方体和球整体为研究对象,竖直方向受重力(m+M)g和地面的支持力FN,水平方向受墙壁的弹力N2和地面的摩擦力Ff,则:
FN=(m+M)g
N2= mgtan45°<Ff
Ff=μFN
联立解得:m<![]() ;
;
(3)a、若球的质量m=![]() M,对整体
M,对整体
FN=(m+M)g
N2= mgtanθ<Ff
Ff=μFN
联立解得:θ<60°
正方体的右侧面AB到墙壁的最大距离:L=R+Rsin60°=![]() R;
R;
b、根据FN=(m+M)g
N2= mgtanθ<Ff
Ff=μFN
得:mgtanθ![]() μ(m+M)g
μ(m+M)g
tanθ![]()
![]()
tanθ![]()
![]() ,θ
,θ![]() 30°
30°
故L![]() R+Rsin30°=
R+Rsin30°=![]() R
R

【题目】在“验证力的平行四边形定则”的实验中,有下列实验步骤:
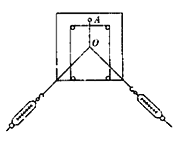
a.在桌上放一块方木板,在方木板上垫一张白纸,把橡皮条的一端固定在板上的A点.
b.只用一只弹簧秤,通过细绳把橡皮条的结点拉到同一位置O,记下弹簧秤的示数![]() 和细绳的方向,按同样一比例做出力
和细绳的方向,按同样一比例做出力![]() 的图示.
的图示.
c.改变两个分力的大小和夹角,再做两次实验.
d.记下两只弹簧秤的示数![]() ,
,![]() 及结点的位置,描下两条细绳的方向,在纸上按比例做出力
及结点的位置,描下两条细绳的方向,在纸上按比例做出力![]() 和
和![]() 的图示,用平行四边形定则求出合力F.
的图示,用平行四边形定则求出合力F.
e.比较力![]() 与
与![]() ,可以看出,它们在实验误差范围内是相等的.
,可以看出,它们在实验误差范围内是相等的.
f.把两条细绳系在橡皮条的另一端,通过细绳用两个弹簧测力计互成角度拉橡皮条,橡皮条伸长,使结点到达某一位置O.
完成下列填空:
(1)上述步骤中,正确的顺序是______(填写步骤前面的字母).
(2)下列哪些措施能减小实验误差______
A.两条细绳必须等长 |
B.弹簧秤、细绳.橡皮条都应与木板平面平行 |
C.拉橡皮条的细绳要稍长一些,标记同一条细绳的方向时两标记点要适当远一些 |
D.实验前先把实验所用的两只弹簧测力计的钩子相互钩住平放在桌面上,向相反方向拉动,检查示数是否相同,若不同.则进行调节使之相同. |