题目内容
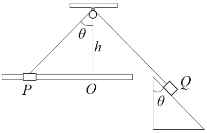
【题目】如图所示,斜面和水平横杆均足够长且均被固定,斜面顶角为θ,套筒P套在横杆上,与轻绳连接,轻绳跨过不计大小的定滑轮,其与放在斜面上的滑块Q相连接,且连接滑块Q的轻绳与斜面平行,P与Q的质量均为m,O为横杆上的滑轮的正下方的点,滑轮到横杆的距离为h。开始时手握住P,使连接P的绳与竖直方向的夹角为θ,然后无初速度释放P。不计绳子的伸长和一切摩擦,重力加速度为g。下列说法正确的是( )
A. 释放P前绳子拉力大小为mgsin θ
B. P到达O点时绳子的拉力为0
C. P到达O点时的速率为![]()
D. P从释放到第一次过O点的过程中,绳子对P的拉力一直做正功
【答案】CD
【解析】
对Q分析,根据共点力平衡求出拉力的大小;根据关联速度的解法分析Q的速度变化情况,从而得出拉力的情况;对P和Q系统研究,结合机械能守恒求出P到达O点的速度大小.根据P点的速度变化,分析动能的变化,从而得拉力做功的情况.
释放P前,对Q分析,根据共点力平衡得![]() ,故A错误。根据P与Q的速度关系
,故A错误。根据P与Q的速度关系![]() ,当P到达O点时
,当P到达O点时![]() ,即
,即![]() ,说明Q先加速后减速,故此时轻绳的拉力不为0,故B错误;当P到达O点时
,说明Q先加速后减速,故此时轻绳的拉力不为0,故B错误;当P到达O点时![]() ,Q减少重力势能与P增加的动能相等,则有:
,Q减少重力势能与P增加的动能相等,则有:![]() ,解得:
,解得: ![]() ,故C正确;P从释放到第一次过O点,速度逐渐增大,动能在增大,故绳子对P的拉力一直做正功,故D正确;故选CD。
,故C正确;P从释放到第一次过O点,速度逐渐增大,动能在增大,故绳子对P的拉力一直做正功,故D正确;故选CD。

练习册系列答案
相关题目