题目内容
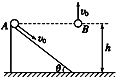
【题目】如图所示,两块半径均为R的半圆形玻璃砖平行正对放置,两圆心的连线OO′水平。一束单色光从左侧A点平行于OO′入射,A到OO'连线的距离为![]() .光从左侧玻璃砖的BC边射出后又从B'C'边的E点射入右侧的玻璃砖(E点未画出),且恰好不能从右侧玻璃砖半圆面射出(不考虑光在各个界面的反射)。已知玻璃折射率n=
.光从左侧玻璃砖的BC边射出后又从B'C'边的E点射入右侧的玻璃砖(E点未画出),且恰好不能从右侧玻璃砖半圆面射出(不考虑光在各个界面的反射)。已知玻璃折射率n=![]() .求:
.求:

(i)光线从BC界面射出时的折射角;
(ⅱ)入射点E点到圆心O'的距离。
【答案】(ⅰ)60° (ⅱ) ![]()
【解析】试题分析:结合题目的要求作出光路图,由折射定律求出光在BC界面上的折射角;根据几何关系求确定光射到弧面上的位置,最后由折射定律,根据几何知识求出O′E的位置。
(ⅰ)作出光路图如图:
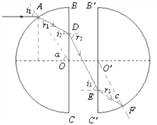
A到 OO′连线的距离为: ![]()
由几何知识得:sinα=![]()
可得入射角: i1=α=60°,
由 ![]() 解得:r1=30°
解得:r1=30°
由几何知识得:i2=30°
根据折射定律: ![]()
解得: r2=60°
(ⅱ)从 E点入射的光线,入射角 i3=r2=60°
根据折射定律: ![]()
解得: r3=30°
光线在 F处发生全反射,则![]()
在△O′EF中,由正弦定理得: 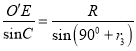
解得: ![]()

练习册系列答案
相关题目