题目内容
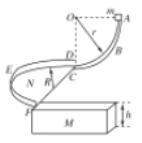
【题目】如图所示,ABC为固定在竖直面内的光滑四分之一圆轨道,其半径为r=10 m,N为固定在水平面内的半圆平面,其半径为R=![]() m,轨道ABC与平面N相切于C点,DEF是包围在半圆平面N周围且垂直于N的光滑半圆形挡板,质量为M=1 kg的长方体滑块的上表面与平面N在同一水平面内,且滑块与N接触紧密但不连接,现让物体自A点由静止开始下滑,进入平面N后受到挡板DEF的约束并最终冲上滑块,已知物体m=1 kg,物体与平面N之间的动摩擦因数为μ1=0.5、与滑块之间的动摩擦因数为μ2=0.4,滑块与地面之间是光滑的,滑块的竖直高度为h=0.05 m,长L=4 m.(取g=10 m/s2)
m,轨道ABC与平面N相切于C点,DEF是包围在半圆平面N周围且垂直于N的光滑半圆形挡板,质量为M=1 kg的长方体滑块的上表面与平面N在同一水平面内,且滑块与N接触紧密但不连接,现让物体自A点由静止开始下滑,进入平面N后受到挡板DEF的约束并最终冲上滑块,已知物体m=1 kg,物体与平面N之间的动摩擦因数为μ1=0.5、与滑块之间的动摩擦因数为μ2=0.4,滑块与地面之间是光滑的,滑块的竖直高度为h=0.05 m,长L=4 m.(取g=10 m/s2)
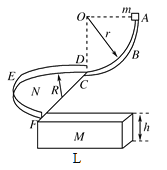
(1)物体滑到C处时对圆轨道的压力是多少?
(2)物体运动到F处时的速度是多少?
(3)当物体从滑块上滑落后到达地面时,物体与滑块之间的距离是多少?
【答案】(1)30 N(2)10 m/s.(3)0.6 m.
【解析】
试题分析:(1)对物体从A处到C处,由机械能守恒定律得mgr=![]() mvC2
mvC2
在C处有F-mg=m![]() ,
,
联立解得F=3mg=30 N
由牛顿第三定律可知,物体滑到C处时,对圆轨道的压力是30 N.
(2)对物体从C处到F处,由动能定理有-μ1mg×πR=![]() mvF2-
mvF2-![]() mvC2
mvC2
解得vF=10 m/s.
(3)物体在滑块上运动,对物体由牛顿第二定律有:
-μ2mg=ma1
解得a1=-4 m/s2
对滑块由牛顿第二定律有:μ2mg=Ma2
解得a2=4 m/s2
设经t时间物体刚要从滑块上滑落,此时物体的速度为v1,滑块的速度为v2.
vFt+![]() a1t2-
a1t2-![]() a2t2=L
a2t2=L
由以上三式得t=![]() s或2 s(不合题意舍去)
s或2 s(不合题意舍去)
则有v1=vF-a1t,v2=a2t
设物体从抛出到落地时间为t1 ,h=![]() gt12
gt12
Δs=v1t1-v2t1=0.6 m.