题目内容
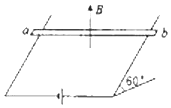
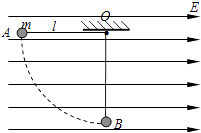
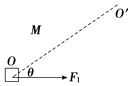
【题目】质量为m，电荷量为q的带负电粒子自静止开始，经M、N板间的电场加速后，从A点垂直于磁场边界射入宽度为d的匀强磁场中，该粒子离开磁场时的位置P偏离入射方向的距离为L，如图所示，已知M、N两板间的电压为U，粒子的重力不计．
（1）正确画出粒子由静止开始至离开匀强磁场时的轨迹图（用直尺和圆规规范作图）；
（2）求匀强磁场的磁感应强度B．
【答案】
（1）解：如图所示：
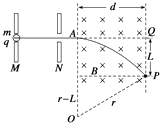
（2）解：设粒子在M、N两板间经电场加速后获得的速度为v，
由动能定理得：qU= 
mv2﹣0 ①，
粒子进入磁场后做匀速圆周运动，设其半径为r，
由牛顿第二定律得：qvB=m 
②
由几何关系得：r2=（r﹣L）2+d2 ③
由①②③解得：B= 
；
答：匀强磁场的磁感应强度B= ．
【解析】解：（1）粒子在电场中做匀加速直线运动，在磁场中做匀速圆周运动，粒子运动轨迹如图所示：
答：（1）粒子由静止开始至离开匀强磁场时的轨迹如图所示；
【考点精析】解答此题的关键在于理解动能定理的综合应用的相关知识，掌握应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷，以及对带电微粒（计重力）在电场中的运动的理解，了解带电颗粒:如液滴、油滴、尘埃、小球等，除有说明或明确的暗示以外，一般都不能忽略重力；由于带电粒子在匀强电场中所受电场力与重力都是恒力，因此可以用两种方法处理:①正交分解法;②等效“重力”法．
练习册系列答案
阅读快车系列答案
相关题目
