题目内容
1.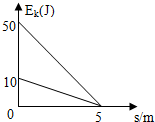 有一物体由某一固定的长斜面的底端以初速度v0沿斜面上滑,斜面与物体间的动摩擦因数μ=0.5,其动能EK随离开斜面底端的距离s变化的图线如图所示,g取10m/s2,不计空气阻力,则以下说法正确的是( )
有一物体由某一固定的长斜面的底端以初速度v0沿斜面上滑,斜面与物体间的动摩擦因数μ=0.5,其动能EK随离开斜面底端的距离s变化的图线如图所示,g取10m/s2,不计空气阻力,则以下说法正确的是( )| A. | 物体在斜面上运动的总时间t=2s | B. | 斜面与物体间的摩擦力大小f=4N | ||
| C. | 物体的质量为m=1kg | D. | 斜面的倾角θ=37° |
分析 对物体进行受力分析,得出物体向上滑动的过程中的受力与物体下滑的过程中的受力,运用动能定理把动能和位移的关系表示出来.
把物理表达式与图象结合起来,根据图象中的数据求出未知物理量.
解答 解:B、C、D、设斜面的倾角是θ,物体的质量是m,物体向上运动的过程中受到重力、支持力和向下的摩擦力;物体向下滑动的过程中受到重力.支持力和向上的摩擦力,由图象可知物体向上滑动的过程中,EK1=50J,EK2=0J,位移x=5m,下滑回到原位置时的动能,EK3=10J
向上滑动的过程中,由动能定理得:EK2-EK1=-mgsinθ•x-fx,
向下滑动的过程中,由动能定理得:EK3-EK2=mgsinθ•x-fx,
代入数据解得:f=4N
mgsinθ=6N
又:f=μmgcosθ
所以:$mgcosθ=\frac{f}{μ}=\frac{4}{0.5}=8N$
$tanθ=\frac{mgsinθ}{mgcosθ}=\frac{3}{4}$
所以:θ=37°
$m=\frac{6}{gsinθ}$kg=1kg.故BCD正确;
A、物体向上时的加速度:${a}_{1}=\frac{-mgsinθ-f}{m}=-10m/{s}^{2}$,
物体向下时的加速度:$a=\frac{mgsinθ-f}{m}=2m/{s}^{2}$,
物体的初速度:${v}_{1}=\sqrt{\frac{2{E}_{k1}}{m}}=10m/s$
物体回到原点的速度:${v}_{\;}=\sqrt{\frac{2{E}_{k12}}{m}}=2\sqrt{5}m/s$
向上运动时间t1=$\frac{0-{v}_{1}}{{a}_{1}}=\frac{-10}{-10}s=1s$
向下运动的时间:${t}_{2}=\frac{v-0}{a}=\sqrt{5}s$
物体在斜面上运动的总时间t=${t}_{1}+{t}_{2}=1+\sqrt{5}s$.故A错误.
故选:BCD
点评 用数学图象处理物理问题的方法就是把物理表达式与图象结合起来,根据图象中的数据求解.一般我们通过图象的特殊值和斜率进行求解.

| A. | 加速度是描述速度变化的物理量 | |
| B. | 速度的变化率就是加速度 | |
| C. | 加速度的方向总与速度的方向相同 | |
| D. | 加速度的方向总与速度变化量的方向相同 |
| A. | 物体运动的时间为$\frac{2{v}_{0}}{g}$ | |
| B. | 该时刻物体的速率等于$\sqrt{5}$v0 | |
| C. | 该时刻物体的水平分速度与竖直分速度相等 | |
| D. | 该时刻物体位移大小等于$\frac{2\sqrt{2}{v}_{0}^{2}}{g}$ |
 雨滴下落中由于空气阻力作用而作匀速下降.汽车静止时,车内的人从矩形车窗ABCD看到窗外雨滴的运动方向如①所示.在汽车从静止开始匀加速启动阶段的t1、t2两个时刻,看到雨滴的运动方向分别如②、③所示.E是AB的中点.则( )
雨滴下落中由于空气阻力作用而作匀速下降.汽车静止时,车内的人从矩形车窗ABCD看到窗外雨滴的运动方向如①所示.在汽车从静止开始匀加速启动阶段的t1、t2两个时刻,看到雨滴的运动方向分别如②、③所示.E是AB的中点.则( )| A. | t2=$\sqrt{2}$t1 | B. | t2=$\sqrt{3}$t1 | C. | t2=2t1 | D. | t2=3t1 |
| A. | 物体能否看做质点,不能由体积的大小判断 | |
| B. | 研究地球的公转时可把地球看作质点 | |
| C. | 研究地球的自转时可把地球看作质点 | |
| D. | 蚂蚁很小,可把蚂蚁看作质点 |
| A. | 物体在5s时指的是物体在5s末时,指的是时间 | |
| B. | 物体在5s内指的是物体在4s末到5s末的这1s的时间 | |
| C. | 物体在第5s内指的是物体在4s末到5s末的这1s的时间 | |
| D. | 第4s末就是第5s初,指的是相差1s的时间 |
 静电计是在验电器基础上制成,用其指针张角的大小来定性显示其金属球与外壳之间电势差大小.如图,A、B是平行板电容器的两个金属板,A板固定,手握B板的绝缘柄,G为静电计.开始时开关S闭合,静电计G指针张开一定角度.则( )
静电计是在验电器基础上制成,用其指针张角的大小来定性显示其金属球与外壳之间电势差大小.如图,A、B是平行板电容器的两个金属板,A板固定,手握B板的绝缘柄,G为静电计.开始时开关S闭合,静电计G指针张开一定角度.则( )| A. | 保持S闭合,只将A、B两板靠近些,G指针张角变小 | |
| B. | 保持S闭合,只将A向上移动,G指针张角变大 | |
| C. | 断开S后,只将A、B两板分开些,G指针张角变小 | |
| D. | 断开S后,只在A、B两板间插入电介质,G指针张角变小 |