题目内容
18.已知电子的质量是9×10-31kg,质子和电子的电荷量均为1.6×10-19C,质子与电子之间的库仑力是9.216×10-8N,电子绕质子做匀速圆周运动,静电力常量k=9×l09N•m2/C2.取$\sqrt{5.12}$=2.26,求:(1)电子转动的半径;
(2)电子转动的速度大小.
分析 (1)根据库仑定律公式F=k$\frac{Qq}{{r}^{2}}$,即可求解;
(2)根据库仑力提供向心力,结合向心力公式,即可求解.
解答 解:(1)由库仑定律,则有:F=k$\frac{Qq}{{r}^{2}}$,
解得:电子转动半径为r=$\sqrt{\frac{9×1{0}^{9}×1.6×1{0}^{-19}×1.6×1{0}^{-19}}{9.216×1{0}^{-8}}}$=5×10-11m
(2)根据质子与电子间的库仑力提供电子转动的向心力,则有:F=$\frac{m{v}^{2}}{r}$
解得:电子转动的速度大小v=$\sqrt{\frac{9.216×1{0}^{-8}×5×1{0}^{-11}}{9×1{0}^{-31}}}$=2.26×106m/s
答:(1)电子转动的半径5×10-11m;
(2)电子转动的速度大小2.26×106m/s.
点评 考查库仑定律与牛顿第二定律的内容,掌握向心力表达式,理解库仑力提供向心力做匀速圆周运动的原理.

练习册系列答案
相关题目
9.一个做匀变速直线运动的质点的v-t图象如图所示,由图线可知( )


| A. | v=(4+2t)m/s | B. | v=(-4+2t)m/s | C. | x=(-4t+t2)m | D. | x=(-4t-t2)m/s |
13.导体处于静电平衡时,下列说法正确的是( )
| A. | 导体内部电场强度一定为0 | |
| B. | 导体的电势一定为0 | |
| C. | 导体表面和内部的电势相等 | |
| D. | 导体表面的电势可能大于内部的电势 |
3. 在科学探究活动中,对实验数据进行分析归纳得出结论是非常重要的环节.为探究物体做直线运动过程中x随t变化的规律,某实验小组经过实验和计算得到下表的实验数据
在科学探究活动中,对实验数据进行分析归纳得出结论是非常重要的环节.为探究物体做直线运动过程中x随t变化的规律,某实验小组经过实验和计算得到下表的实验数据
(1)现根据表格数据,请你在如图所示的坐标系中,纵、横轴分别选择合适的物理量和标度作出关系图线.
(2)请你根据你作出的图线,分析得出物体从A→B的过程中x随t2变化的规律是s=0.31t2.
 在科学探究活动中,对实验数据进行分析归纳得出结论是非常重要的环节.为探究物体做直线运动过程中x随t变化的规律,某实验小组经过实验和计算得到下表的实验数据
在科学探究活动中,对实验数据进行分析归纳得出结论是非常重要的环节.为探究物体做直线运动过程中x随t变化的规律,某实验小组经过实验和计算得到下表的实验数据| 物体运动的起止点 | 所测的 物理量 | 测量次数 | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| A→B | 时间t(s) | 0.89 | 1.24 | 1.52 | 1.76 | 1.97 |
| 时间二次方 t2(s2) | 0.79 | 1.54 | 2.31 | 3.10 | 3.88 | |
| 位移x(m) | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | |
(2)请你根据你作出的图线,分析得出物体从A→B的过程中x随t2变化的规律是s=0.31t2.
8. 一皮带传送装置如图所示,轻弹簧一端固定,另一端连接一个质量为m的滑块,已知滑块与皮带之间存在摩擦.现将滑块轻放在皮带上,弹簧恰好处于自然长度且轴线水平.若在弹簧从自然长度到第一次达到最长的过程中,滑块始终未与皮带达到共速,则在此过程中滑块的速度和加速度变化情况是( )
一皮带传送装置如图所示,轻弹簧一端固定,另一端连接一个质量为m的滑块,已知滑块与皮带之间存在摩擦.现将滑块轻放在皮带上,弹簧恰好处于自然长度且轴线水平.若在弹簧从自然长度到第一次达到最长的过程中,滑块始终未与皮带达到共速,则在此过程中滑块的速度和加速度变化情况是( )
 一皮带传送装置如图所示,轻弹簧一端固定,另一端连接一个质量为m的滑块,已知滑块与皮带之间存在摩擦.现将滑块轻放在皮带上,弹簧恰好处于自然长度且轴线水平.若在弹簧从自然长度到第一次达到最长的过程中,滑块始终未与皮带达到共速,则在此过程中滑块的速度和加速度变化情况是( )
一皮带传送装置如图所示,轻弹簧一端固定,另一端连接一个质量为m的滑块,已知滑块与皮带之间存在摩擦.现将滑块轻放在皮带上,弹簧恰好处于自然长度且轴线水平.若在弹簧从自然长度到第一次达到最长的过程中,滑块始终未与皮带达到共速,则在此过程中滑块的速度和加速度变化情况是( )| A. | 速度一直增大 | B. | 速度先增大后减小 | ||
| C. | 加速度先增大后减小 | D. | 加速度先减小后增大 |

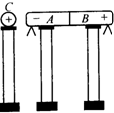 如图所示,在研究感应起电的实验中,A、B为相互接触的用绝缘支柱支持的金属导体,起初它们不带电,在它们的下部贴有金属箔片,C是带正电的小球,当进行下列操作时会看到怎样的现象?(填“张开”或“闭合”)
如图所示,在研究感应起电的实验中,A、B为相互接触的用绝缘支柱支持的金属导体,起初它们不带电,在它们的下部贴有金属箔片,C是带正电的小球,当进行下列操作时会看到怎样的现象?(填“张开”或“闭合”) 在如图所示电路中,电源电动势E=15V、内阻r=1.0Ω,定值电阻R1=29Ω,R2=30Ω,R3=60Ω.当开关闭合后,电阻R3上消耗的电功率是多大?
在如图所示电路中,电源电动势E=15V、内阻r=1.0Ω,定值电阻R1=29Ω,R2=30Ω,R3=60Ω.当开关闭合后,电阻R3上消耗的电功率是多大? 悬挂在O点的一根不可伸长的绝缘细线下端有一个质量为m、带电量为-q的小球,若在空间加一水平方向的匀强电场,则小球静止时细线与竖直方向夹角为θ,如图所示,求:所加匀强电场场强的大小和方向.
悬挂在O点的一根不可伸长的绝缘细线下端有一个质量为m、带电量为-q的小球,若在空间加一水平方向的匀强电场,则小球静止时细线与竖直方向夹角为θ,如图所示,求:所加匀强电场场强的大小和方向.