题目内容
如图所示为某种透明介质的截面图，△AOC为等腰直角三角形，BC为半径R＝10cm的四分之一圆弧，AB与水平屏幕MN垂直并接触于A点．由红光和紫光两种单色光组成的复色光射向圆心O，在AB分界面上的入射角i＝45°，结果在水平屏幕MN上出现两个亮斑．已知该介质对红光和紫光的折射率分别为n1＝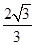
，n2＝
.
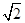(1)判断在AM和AN两处产生亮斑的颜色；
(2)求两个亮斑间的距离．
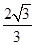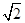，n2＝.(1)判断在AM和AN两处产生亮斑的颜色；
(2)求两个亮斑间的距离．
(1) 在AM处产生的亮斑P1为红色，在AN处产生的亮斑P2为红色和紫色的混合色 (2)(5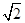＋10)cm
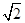＋10)cm试题分析：(1)设红光和紫光的临界角分别为C1、C2，sinC1＝
＝
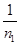，C1＝60°，同理C2＝45°，i＝45°＝C2，i＝45°<C1，所以紫光在AB面发生全反射，而红光在AB面一部分折射，一部分反射，且由几何关系可知，反射光线与AC垂直，所以在AM处产生的亮斑P1为红色，在AN处产生的亮斑P2为红色和紫色的混合色．
(2)画出如图所示光路图，
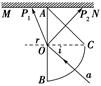
设折射角为r，两个光斑分别为P1、P2，根据折射定律n1＝
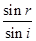求得sinr＝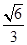
由几何知识可得：tanr＝
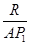，解得AP1＝5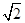cm.由几何知识可得△OAP2为等腰直角三角形，解得AP2＝10cm，所以P1P2＝(5
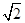＋10)cm.
练习册系列答案
相关题目
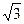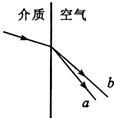
×108m/s,要使光由空气射入这种玻璃时,折射光线与反射光线之间成900角，则入射角是多少？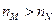
，两束单色光a、b入射到M的上表面，经折射后形成复合光束c，则下列说法正确的是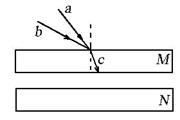
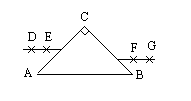
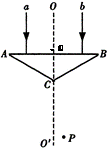如图所示，A、B、C为等腰棱镜，a、b两束不同频率的单色光垂直AB边射入棱镜，两束光在AB面上的入射点到D的距离相等，两束光通过棱镜折射后相交于图中的P点，以下判断正确的是（ ）
