题目内容
如图所示,左图是游乐场中过山车的实物图片,右图是过山车的原理图.在原理图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道,固定在倾角为α=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使小车(视作质点)从P点以一定的初速度沿斜面向下运动.已知斜轨道面与小车间的动摩擦因数为μ=
.问:(已知:g=10m/s2,sin37°=0.6,cos37°=0.8,tan(
)=
.结果可保留根号.)
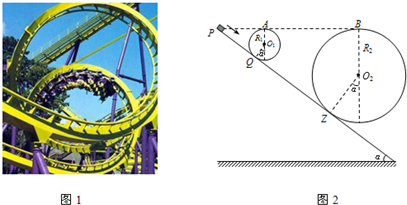
(1)若小车恰好能通过第一个圆形轨道的最高点A处,则其在P点的初速度应为多大?
(2)若小车在P点的初速度为10m/s,则小车能否安全通过两个圆形轨道?
| 1 |
| 24 |
| a |
| 2 |
| sina |
| 1+cosa |

(1)若小车恰好能通过第一个圆形轨道的最高点A处,则其在P点的初速度应为多大?
(2)若小车在P点的初速度为10m/s,则小车能否安全通过两个圆形轨道?
(1)小车恰好过A点,由牛顿第二定律有
mg=m
小球P到A的过程中,由动能定理有
-μmgcosα?SPQ=
m
-
m
由几何关系可得SPQ=
代入数据可得v0=2
m/s
(2)小车以v=10m/s的初速度从P点下滑时,因为有v=10m/s>v0=2
m/s
所以小车可以通过圆弧轨道O1,设小车恰好能通过B点,
由牛顿第二定律有 mg=m
则P到B由动能定理得
-μmgcosα?SPZ=
m
-
m
其中 SPZ=
代入数据可得 vP=
m/s
因为vP=
m/s<10m/s,所以小车能安全通过两个圆形轨道.
答:
(1)若小车恰好能通过第一个圆形轨道的最高点A处,则其在P点的初速度应为2
m/s;
(2)若小车在P点的初速度为10m/s,小车能安全通过两个圆形轨道.
mg=m
| ||
| R1 |
小球P到A的过程中,由动能定理有
-μmgcosα?SPQ=
| 1 |
| 2 |
| v | 2A |
| 1 |
| 2 |
| v | 20 |
由几何关系可得SPQ=
| R1(1+cosα) |
| sinα |
代入数据可得v0=2
| 6 |
(2)小车以v=10m/s的初速度从P点下滑时,因为有v=10m/s>v0=2
| 6 |
所以小车可以通过圆弧轨道O1,设小车恰好能通过B点,
由牛顿第二定律有 mg=m
| ||
| R2 |
则P到B由动能定理得
-μmgcosα?SPZ=
| 1 |
| 2 |
| v | 2B |
| 1 |
| 2 |
| v | 2P |
其中 SPZ=
| R2(1+cosα) |
| sinα |
代入数据可得 vP=
| 96 |
因为vP=
| 96 |
答:
(1)若小车恰好能通过第一个圆形轨道的最高点A处,则其在P点的初速度应为2
| 6 |
(2)若小车在P点的初速度为10m/s,小车能安全通过两个圆形轨道.

练习册系列答案
相关题目






