题目内容
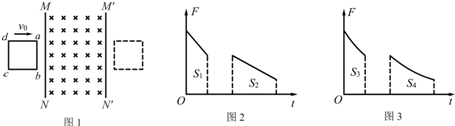
如图1所示,虚线MN、M′N′为一匀强磁场区域的左右边界,磁场宽度为L,方向竖直向下.边长为l的正方形闭合金属线框abcd,以初速度v0沿光滑绝缘水平面向磁场区域运动,经过一段时间线框通过了磁场区域.已知l<L,甲、乙两位同学对该过程进行了分析,当线框的ab边与MN重合时记为t=0,分别定性画出了线框所受安培力F随时间t变化的图线,如图2、图3所示,图中S1、S2、S3和S4是图线与t轴围成的面积.关于两图线的判断以及S1、S2、S3和S4应具有的大小关系,下列说法正确的是( )

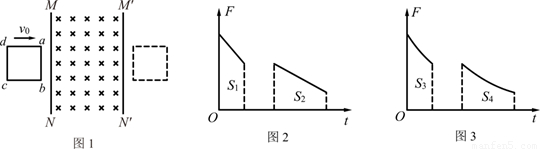
| A.图2正确,且S1>S2 | B.图2正确,且S1=S2 |
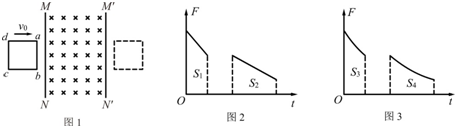
| C.图3正确,且S3>S4 | D.图3正确,且S3=S4 |
(1)设切割磁感线的速度是v,产生的电流为I,电动势为E,则:
E=Blv,I=
,
则:F=BIl=
导体棒上的加速度:a=
=
在电磁感应的过程中,动能转化为电能,速度减小,安培力减小,加速度减小,所以导体棒做加速度减小的减速运动,故F-t图上,F的变化是曲线,不是直线.
(2)在图象中,F与t的积表示的是面积S,公式:
Ft=
t=
t
l=
从公式可以看出,F与t的积是一个定值,即面积的大小与时间无关,是一个定值,故S3=S4是正确的.
综合(1)和(2)的结论,正确的选项应该是D.
故选:D
E=Blv,I=
| E |
| R |
则:F=BIl=
| B2l2v |
| R |
导体棒上的加速度:a=
| E |
| R |
| B2l2v |
| R2 |
在电磁感应的过程中,动能转化为电能,速度减小,安培力减小,加速度减小,所以导体棒做加速度减小的减速运动,故F-t图上,F的变化是曲线,不是直线.
(2)在图象中,F与t的积表示的是面积S,公式:
Ft=
| B2l2v |
| R |
| B2l2 |
| R |
| . |
| v |
| B2l2 |
| R |
| B2l3 |
| R |
从公式可以看出,F与t的积是一个定值,即面积的大小与时间无关,是一个定值,故S3=S4是正确的.
综合(1)和(2)的结论,正确的选项应该是D.
故选:D

练习册系列答案
相关题目