题目内容
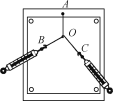
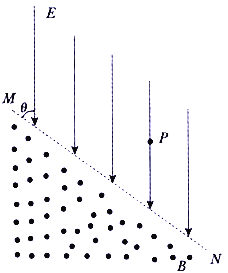
【题目】如图所示，虚线MN为匀强电场和匀强磁场的分界线，匀强电场场强大小为E方向竖直向下且与边界MN成
=45°角，匀强磁场的磁感应强度为B，方向垂直纸面向外，在电场中有一点P，P点到边界MN的竖直距离为d。现将一质量为m、电荷量为q的带正电粒子从P处由静止释放（不计粒子所受重力，电场和磁场范围足够大）。求：
（1）粒子第一次进入磁场时的速度大小；
（2）粒子第一次出磁场处到第二次进磁场处的距离；
（3）若粒子第一次进入磁场后的某时刻，磁感应强度大小突然变为
，但方向不变，此后粒子恰好被束缚在该磁场中，则的最小值为多少？
【答案】（1）
（2）
（3）
【解析】
（1）设粒子第一次进入磁场时的速度大小为v，由动能定理可得
，
解得
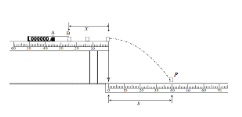
（2）粒子在电场和磁场中的运动轨迹如图所示，粒子第一次出磁场到第二次进磁场，两点间距为
由类平抛规律
，
由几何知识可得x=y，解得
两点间的距离为
，代入数据可得
（3）由
可得
，即
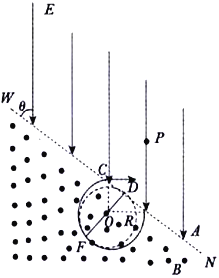
由题意可知，当粒子运动到F点处改变磁感应强度的大小时，粒子运动的半径又最大值，即
最小，粒子的运动轨迹如图中的虚线圆所示。
设此后粒子做圆周运动的轨迹半径为r，则有几何关系可知
又因为
，所以
，
代入数据可得
练习册系列答案
相关题目
