题目内容
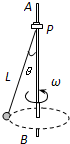
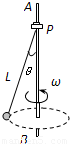
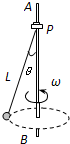 如图所示,竖直杆AB上的P点用细线悬挂着一个小铅球,球的半径相对线长可忽略不计,已知线长为L=1.25m.当AB杆绕自身以ω=4rad/s转动时,小球在细线的带动下在水平面上做圆锥摆运动.求细线与杆AB间的夹角θ的大小.(g=10m/s2)
如图所示,竖直杆AB上的P点用细线悬挂着一个小铅球,球的半径相对线长可忽略不计,已知线长为L=1.25m.当AB杆绕自身以ω=4rad/s转动时,小球在细线的带动下在水平面上做圆锥摆运动.求细线与杆AB间的夹角θ的大小.(g=10m/s2)分析:对小球进行受力分析,合外力提供向心力,根据向心力公式及半径与线长的关系即可求解.
解答: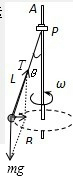 解:对小球进行受力分析,如图所示:
解:对小球进行受力分析,如图所示:
则有:Fn=mgtanθ=mω2r
又有:r=Lsinθ
由以上两式得:
cosθ=
=
所以θ=60°
答:细线与杆AB间的夹角θ为60°
 解:对小球进行受力分析,如图所示:
解:对小球进行受力分析,如图所示:则有:Fn=mgtanθ=mω2r
又有:r=Lsinθ
由以上两式得:
cosθ=
| g |
| ω2L |
| 1 |
| 2 |
所以θ=60°
答:细线与杆AB间的夹角θ为60°
点评:本题主要考查了向心力公式的直接应用,要求同学们能正确对小球进行受力分析,找出向心力的来源,难度不大,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
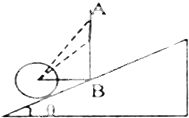 如图所示,竖直杆AB固定在斜面上,小球用细绳系在倾角为θ的光滑斜面上,保持小球不动,当细绳方向由水平逐渐向上偏移时,绳的拉力F和斜面对小球的支持力FN将( )
如图所示,竖直杆AB固定在斜面上,小球用细绳系在倾角为θ的光滑斜面上,保持小球不动,当细绳方向由水平逐渐向上偏移时,绳的拉力F和斜面对小球的支持力FN将( )