题目内容
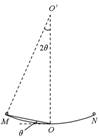
 如图所示的MON是曲率半径很大的圆弧形轨道,所对的圆心角很小,O是轨道的最低点,M、N两点等高.连接OM的一段直线轨道顶端的M点有一块小滑块从静止开始沿着直线轨道下滑;同时,从N点也有一块小滑块从静止开始沿着圆弧轨道下滑.如果不计一切摩擦,则( )
如图所示的MON是曲率半径很大的圆弧形轨道,所对的圆心角很小,O是轨道的最低点,M、N两点等高.连接OM的一段直线轨道顶端的M点有一块小滑块从静止开始沿着直线轨道下滑;同时,从N点也有一块小滑块从静止开始沿着圆弧轨道下滑.如果不计一切摩擦,则( )分析:由于MON是曲率半径很大的圆弧形轨道,从N点下滑的小滑块做简谐运动,运动时间是
周期.从M点沿直线下滑的物体做匀加速直线运动,由牛顿第二定律和运动学公式求出时间,比较两滑块运动时间的长短,确定相遇的位置.
| 1 |
| 4 |
解答:解:设圆弧形轨道为R,所对的圆心角为2α.
设,从N点下滑的滑块运动到最低点的时间为t1,从M点下滑的滑块运动到最低点的时间为t2.
则
对于左侧滑块:加速度大小a=gsinα
x=
a
根据几何知识,x≈Rsinα
t2=
=
=
对于右侧滑块:t1=
=
?2π
=
可见,t1>t2.
所以两个滑块一定在O点左方相遇.
故选B
设,从N点下滑的滑块运动到最低点的时间为t1,从M点下滑的滑块运动到最低点的时间为t2.
则
对于左侧滑块:加速度大小a=gsinα
x=
| 1 |
| 2 |
| t | 2 2 |
根据几何知识,x≈Rsinα
t2=
|
|
|
对于右侧滑块:t1=
| T |
| 4 |
| 1 |
| 4 |
|
|
可见,t1>t2.
所以两个滑块一定在O点左方相遇.
故选B
点评:本题右侧滑块的运动可等效于摆长为R的单摆,当圆心很小,小于10°时,其振动是简谐运动,周期为T=2π
.
|

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目