题目内容
3.身高为2m的宇航员,用背越式跳高,在地球上能跳2.21m,在某一未知星球上能跳5.84m,已知该星球的半径与地球的半径相同,忽略自转的影响,地球表面重力加速度为g,则( )| A. | 该星球表面重力加速度约为$\frac{1}{4}$g | |
| B. | 卫星围绕该星期运动的最大环绕速度是地球第一宇宙速度的2倍 | |
| C. | 该星球密度与地球的密度相等 | |
| D. | 该星球上同步卫星的运动周期是48小时 |
分析 应用匀变速直线运动的速度位移公式求出重力加速度,然后求出星球表面的重力加速度,然后应用牛顿第二定律分析答题.
解答 解:A、背越式跳高运动员在竖直方向上做竖直上抛运动,h=$\frac{{v}_{0}^{2}}{2g}$,则:g=$\frac{{v}_{0}^{2}}{2h}$,$\frac{{g}_{星}}{g}$=$\frac{{h}_{地}}{{h}_{星}}$=$\frac{2.21-1}{5.84-1}$=$\frac{1}{4}$,故A正确;
B、卫星做圆周运动,万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{R}^{2}}$=mg=m$\frac{{v}^{2}}{R}$,解得:v=$\sqrt{gR}$,$\frac{{v}_{星}}{{v}_{地}}$=$\frac{\sqrt{R{g}_{星}}}{\sqrt{R{g}_{地}}}$=$\frac{1}{2}$,故B错误;
C、重力等于万有引力,即:G$\frac{Mm}{{R}^{2}}$=mg,解得:M=$\frac{g{R}^{2}}{G}$,密度:ρ=$\frac{M}{\frac{4}{3}π{R}^{3}}$=$\frac{3g}{4πGR}$,密度之比:$\frac{{ρ}_{星}}{{ρ}_{地}}$=$\frac{{g}_{星}}{{g}_{地}}$=$\frac{1}{4}$,故C错误;
D、加速度:g=$(\frac{2π}{T})^{2}$R,则:T=2π$\sqrt{\frac{R}{g}}$,$\frac{{T}_{星}}{{T}_{地}}$=$\sqrt{\frac{{g}_{地}}{{g}_{星}}}$=2,则该星球的同步卫星周期为:24×2=48h,故D正确;
故选:AD.
点评 本题考查了万有引力定律的应用,知道万有引力等于重力、万有引力提供向心力是正确解题的关键,应用万有引力公式、牛顿第二定律与竖直上抛运动规律可以解题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,一个电量为+Q的点电荷甲,固定在绝缘平面上的O点.另一个电量为-q及质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点静止.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为s.下列说法正确的是( )
如图所示,一个电量为+Q的点电荷甲,固定在绝缘平面上的O点.另一个电量为-q及质量为m的点电荷乙,从A点以初速度v0沿它们的连线向甲运动,运动到B点静止.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为s.下列说法正确的是( )| A. | OB间的距离为$\sqrt{\frac{kQq}{μmg}}$ | |
| B. | 滑块从A到B的运动过程中,中间时刻的速度小于$\frac{v_0}{2}$ | |
| C. | 从A到B的过程中,产生的内能为$\frac{mv_0^2}{2}$ | |
| D. | Q产生的电场中,A、B两点间的电势差为UAB=$\frac{m(v_0^2-2μgs)}{2q}$ |
 某兴趣小组用实验室的手摇发电机和一个可看作理想的小变压器给一个灯泡供电,电路如图,当线圈以较大的转速n匀速转动时,额定电压为U0的灯泡正常发光,电压表示数是U1.已知线圈电阻是r,灯泡电阻是R,则有( )
某兴趣小组用实验室的手摇发电机和一个可看作理想的小变压器给一个灯泡供电,电路如图,当线圈以较大的转速n匀速转动时,额定电压为U0的灯泡正常发光,电压表示数是U1.已知线圈电阻是r,灯泡电阻是R,则有( )| A. | 变压器输入电压的瞬时值是u=U1sin2πnt | |
| B. | 变压器的原副线圈匝数比是U0:U1 | |
| C. | 电流表的示数是$\frac{{{U}_{0}}^{2}}{R{U}_{1}}$ | |
| D. | 线圈中产生的电动势最大值是Em=$\sqrt{2}$U1 |
 如图所示,小球从高处下落到竖直放置的轻弹簧上,在小球接触弹簧到将弹簧压缩到最短的整个过程中,下列叙述正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,在小球接触弹簧到将弹簧压缩到最短的整个过程中,下列叙述正确的是( )| A. | 小球动能先减小后增大 | |
| B. | 小球动能不断减小 | |
| C. | 动能和弹性势能之和总保持不变 | |
| D. | 重力势能、弹性势能和动能之和总保持不变 |
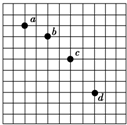 (1)在做“研究平抛运动”实验时,除了木板、小球、斜槽、铅笔、图钉之外,下列器材中还需要的是CF.
(1)在做“研究平抛运动”实验时,除了木板、小球、斜槽、铅笔、图钉之外,下列器材中还需要的是CF.