题目内容
6.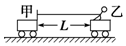 如图所示,甲、乙两车的质量均为M,静置在光滑的水平面上,两车相距为L,乙车上站立着一个质量为m的人,他通过一条水平轻绳用恒定的拉力F拉甲车直到两车相碰,在此过程中( )
如图所示,甲、乙两车的质量均为M,静置在光滑的水平面上,两车相距为L,乙车上站立着一个质量为m的人,他通过一条水平轻绳用恒定的拉力F拉甲车直到两车相碰,在此过程中( )| A. | 甲、乙两车运动过程中的速度之比为(M+m):M | |
| B. | 甲车移动的距离为$\frac{M+m}{2M+m}L$ | |
| C. | 此过程中人拉绳所做功为FL | |
| D. | 此过程中人拉绳所做功为$\frac{M+m}{2M+m}FL$ |
分析 乙通过一条轻绳拉甲车的过程,甲、乙和两车组成的系统合外力为零,系统的动量守恒,由动量守恒定律求甲、乙两车运动中速度之比.将速度由位移与时间之比表示,代入动量守恒定律表达式,并结合几何关系可求两车移动的距离.根据功的定义即可求出拉绳做的功.
解答 解:A、甲、乙和两车组成的系统合外力为零,系统的动量守恒,取向右为正方向,由动量守恒定律得:
0=Mv甲-(M+m)v乙;
可得甲、乙两车运动中速度之比为:$\frac{{v}_{甲}}{{v}_{乙}}$=$\frac{M+m}{M}$,故A正确;
B、设甲车和乙车移动的距离分别为s1和s2.则有:v甲=$\frac{{s}_{甲}}{t}$,v乙=$\frac{{s}_{乙}}{t}$
又 s1+s2=L
联立解得:s1=$\frac{M+m}{2M+m}$L,s2=$\frac{M}{2M+m}$L,故B正确;
CD、根据功的定义可知,此过程中人拉绳所做功等于拉力和人相对于绳子的位移的乘积,为W=FL.故C正确,D错误
故选:ABC
点评 解决本题的关键要把握系统的动量守恒,运用速度公式表示速度与位移的关系,要注意速度和位移的参照物都是地面.
同时要注意的另一个问题是拉绳子的力做的功:人拉绳子的过程中人对绳子做的功转化为绳子对甲做的功以及绳子对乙和人做功的和,所以人拉绳子做的功是FL而不是$\frac{M+m}{2M+m}FL$.要理解该过程中的功能关系的转化.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
19.下列说法正确的是( )
| A. | 所有的固体都有固定的熔点,物理性质各向异性 | |
| B. | 气体从外界吸收热量,其内能不一定增加 | |
| C. | 布朗运动就是液体分子的无规则运动 | |
| D. | 荷叶上的水珠之所以表现为球状,是因为液体表面张力作用的结果 | |
| E. | 当两个分子处于平衡状态时,分子势能最小 |
1.对向心力的两个公式①F=mω2r和②F=m$\frac{{v}^{2}}{r}$的理解,下列说法中正确的是( )
| A. | 两个公式都表明在其他条件不变时,做匀速圆周运动的物体所需向心力与物体质量m成正比 | |
| B. | 公式①表明向心力跟半径r成正比 | |
| C. | 公式②表明向心力跟半径r成反比 | |
| D. | 公式①表明在角速度不变的情况下,向心力跟圆半径r成正比 |
11.关于近代物理内容的若干叙述,下列说法正确的是( )
| A. | 普朗克引入能量子的概念,得出黑体辐射的强度按波长分布的公式,与实验符合得非常好,并由此开创了物理学的新纪元 | |
| B. | 汤姆逊通过α粒子散射实验,提出了原子具有核式结构 | |
| C. | 根据爱因斯坦的光电效应理论,一束光照射到某种金属上不能发生光电效应,改用波长较长的光照射该金属可能发生 | |
| D. | 根据波尔理论,氢原子放出一个光子,其核外电子的运动半径增大 |
17.机械运动在介质中传播形成机械波.下列说法正确的是( )
| A. | 如果波源停止振动,在介质中传播的波动也立即停止 | |
| B. | 在纵波中质点的振动方向总是垂直于波的传播方向 | |
| C. | 在横波中两个相邻的波峰(或波谷)之间的距离等于波长 | |
| D. | 横波中振动质点不随波迁移,纵波中振动质点随波迁移 |
14. 如图所示,把三个半径均为r,质量均为m的光滑小球置于截面为半圆形的槽内,三个小球均处于静止状态,已知槽的截面半径R=3r,重力加速度为g,则下列说法正确的是( )
如图所示,把三个半径均为r,质量均为m的光滑小球置于截面为半圆形的槽内,三个小球均处于静止状态,已知槽的截面半径R=3r,重力加速度为g,则下列说法正确的是( )
 如图所示,把三个半径均为r,质量均为m的光滑小球置于截面为半圆形的槽内,三个小球均处于静止状态,已知槽的截面半径R=3r,重力加速度为g,则下列说法正确的是( )
如图所示,把三个半径均为r,质量均为m的光滑小球置于截面为半圆形的槽内,三个小球均处于静止状态,已知槽的截面半径R=3r,重力加速度为g,则下列说法正确的是( )| A. | 三个小球与槽之间的作用力大小相等 | |
| B. | 球1与槽之间的作用力大小为mg | |
| C. | 球2与槽之间的作用力大小为3mg | |
| D. | 若仅增大槽的半径R,则球2与槽之间的作用力增大 |
14.跳高比赛中,必须在运动员着地处铺上很厚的海绵垫子,这是为了( )
| A. | 减小运动员着地过程中受到的冲量作用 | |
| B. | 减小运动员着地过程中受到的平均冲力 | |
| C. | 减小运动员着地过程中动量的变化量 | |
| D. | 减小运动员的惯性 |
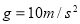 );若以相等时间间隔在该直尺的另一面标记出表示反应时间的刻度线,则每个时间间隔在直尺上对应的长度是_________的(填“相等”或“不相等”)
);若以相等时间间隔在该直尺的另一面标记出表示反应时间的刻度线,则每个时间间隔在直尺上对应的长度是_________的(填“相等”或“不相等”)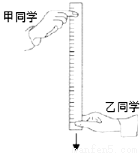
 平行金属板MN和OP水平正对放置,板长为2l,板间距为l,虚线NP右侧足够大的空间有垂直纸面向里的匀强磁场.现以O为坐标原点,沿OM方向建立坐标轴oy.质量为m、电量为+q的带电粒子(不计重力)可以分别从oy轴上O、M间任意点(包含O、M两点)以相同的水平速度v0射入板间,每个粒子单独射入,每个粒子在板间运动过程中板间电压保持恒定,且认为电场只分布在两板之间的区域;射入点不同的粒子偏转电压不同,以确保从y轴上O、M间任意位置水平射入的粒子,均恰好到达P点并离开电场进入磁场.求:
平行金属板MN和OP水平正对放置,板长为2l,板间距为l,虚线NP右侧足够大的空间有垂直纸面向里的匀强磁场.现以O为坐标原点,沿OM方向建立坐标轴oy.质量为m、电量为+q的带电粒子(不计重力)可以分别从oy轴上O、M间任意点(包含O、M两点)以相同的水平速度v0射入板间,每个粒子单独射入,每个粒子在板间运动过程中板间电压保持恒定,且认为电场只分布在两板之间的区域;射入点不同的粒子偏转电压不同,以确保从y轴上O、M间任意位置水平射入的粒子,均恰好到达P点并离开电场进入磁场.求: