题目内容
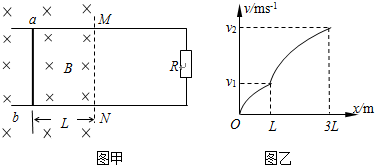 (2011?江苏模拟)如图甲所示,光滑平行金属导轨水平放置,间距为L,导轨一部分处在垂直导轨平面向下的匀强磁场中,MN为磁场边界,磁感应强度为B,导轨右侧接有定值电阻R,导轨电阻忽略不计.在距离MN为L的处垂直导轨放置一根质量为m、电阻为r的金属杆ab.试求:(1)若固定a b杆,磁场按Bt=Bcosωt规律由B减小到零,在此过程中电阻R上产生的电热Q1是多少;
(2011?江苏模拟)如图甲所示,光滑平行金属导轨水平放置,间距为L,导轨一部分处在垂直导轨平面向下的匀强磁场中,MN为磁场边界,磁感应强度为B,导轨右侧接有定值电阻R,导轨电阻忽略不计.在距离MN为L的处垂直导轨放置一根质量为m、电阻为r的金属杆ab.试求:(1)若固定a b杆,磁场按Bt=Bcosωt规律由B减小到零,在此过程中电阻R上产生的电热Q1是多少;(2)若磁感应强度大小保持B大小不变,用水平向右的恒力使ab杆由静止开始向右运动,其速度-位移的关系图象如图乙所示,则ab杆在离开磁场前瞬间的加速度为多大;在ab杆滑过3L的过程中电阻R上产生的电热Q2是多少?.
分析:根据法拉第电磁感应定律求出线框中感应电动势.
根据焦耳定律和正弦交变电流的特点求出电阻R上产生的焦耳热Ql.
对金属杆ab进行受力分析和运动过程分析,应用动能定理研究从L到3L的过程,表示出恒力F.
对金属杆ab刚要离开磁场时进行受力分析,运用牛顿第二定律列出等式求出加速度.
运用动能定理研究由起始位置到发生位移L的过程,求出安培力做功.
根据功能关系知道克服安培力做功求出电路中产生的焦耳热.
根据焦耳定律和正弦交变电流的特点求出电阻R上产生的焦耳热Ql.
对金属杆ab进行受力分析和运动过程分析,应用动能定理研究从L到3L的过程,表示出恒力F.
对金属杆ab刚要离开磁场时进行受力分析,运用牛顿第二定律列出等式求出加速度.
运用动能定理研究由起始位置到发生位移L的过程,求出安培力做功.
根据功能关系知道克服安培力做功求出电路中产生的焦耳热.
解答:解:(1)当磁场按Bt=Bcosωt规律变化时,回路中产生的电动势大小为
e=
L2=BL2ωsin?t
其有效值为 E=
磁场由B减小到零经历的时间为 t=
=
在此过程中,电阻R产生的热量 Q1=(
)2Rt=
(2)设恒定的拉力大小为F,在ab杆离开磁场区的瞬间,牛顿第二定律:F-
=ma
在ab杆在磁场运动过程中,由动能定理F?l-Q2=
m
在ab杆离开磁场继续向前运动2L的过程中:F?2L=
m(
-
)
联立上述三个等式可得:a=
-
Q2=
m(
-3
)
答:(1)若固定a b杆,磁场按Bt=Bcosωt规律由B减小到零,在此过程中电阻R上产生的电热Q1是
;
(2)ab杆在离开磁场前瞬间的加速度为
-
;
在ab杆滑过3L的过程中电阻R上产生的电热Q2是
m(
-3
).
e=
| △B |
| △t |
其有效值为 E=
| BL2ω | ||
|
磁场由B减小到零经历的时间为 t=
| 1 |
| 4 |
| 2π |
| ω |
| π |
| 2ω |
在此过程中,电阻R产生的热量 Q1=(
| E |
| R+r |
| πωRB2L4 |
| 4(R+r)2 |
(2)设恒定的拉力大小为F,在ab杆离开磁场区的瞬间,牛顿第二定律:F-
| B2L2v1 |
| R+r |
在ab杆在磁场运动过程中,由动能定理F?l-Q2=
| 1 |
| 2 |
| v | 2 1 |
在ab杆离开磁场继续向前运动2L的过程中:F?2L=
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
联立上述三个等式可得:a=
| ||||
| 4L |
| B2L2v1 |
| m(R+r) |
Q2=
| 1 |
| 4 |
| v | 2 2 |
| v | 2 1 |
答:(1)若固定a b杆,磁场按Bt=Bcosωt规律由B减小到零,在此过程中电阻R上产生的电热Q1是
| πωRB2L4 |
| 4(R+r)2 |
(2)ab杆在离开磁场前瞬间的加速度为
| ||||
| 4L |
| B2L2v1 |
| m(R+r) |
在ab杆滑过3L的过程中电阻R上产生的电热Q2是
| 1 |
| 4 |
| v | 2 2 |
| v | 2 1 |
点评:要能够把法拉第电磁感应定律与电路知识结合运用.
电磁感应中动力学问题离不开受力分析和运动过程分析.
关于电磁感应中能量问题我们要从功能关系角度出发研究.
电磁感应中动力学问题离不开受力分析和运动过程分析.
关于电磁感应中能量问题我们要从功能关系角度出发研究.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 (2011?江苏模拟)如图所示电路,将两个相同的电流计分别改装成电流表A1(0~3A)和电流表A2(0~0.6A),把这两个电流表并连接入电路中测量电流.则下列说法中正确的是( )
(2011?江苏模拟)如图所示电路,将两个相同的电流计分别改装成电流表A1(0~3A)和电流表A2(0~0.6A),把这两个电流表并连接入电路中测量电流.则下列说法中正确的是( )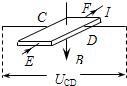 (2011?江苏模拟)利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,C、D两侧面会形成电势差UCD,下列说法中正确的是( )
(2011?江苏模拟)利用霍尔效应制作的霍尔元件,广泛应用于测量和自动控制等领域.如图是霍尔元件的工作原理示意图,磁感应强度B垂直于霍尔元件的工作面向下,通入图示方向的电流I,C、D两侧面会形成电势差UCD,下列说法中正确的是( )