题目内容
如图所示，竖直固定的光滑绝缘细杆，跟一以带电量为Q的正点电荷为圆心、半径为r的圆周交于C、D两点，弦长CD与r相等，一质量为m、带电量为-q的有孔小球套在细杆上，且从杆上的P点由静止开始下滑，已知q?Q，PC=h，可看作点电荷的小球滑到C点时速度大小为vC=| 3gh |
（1）小球到达C点时的加速度和细杆所受的压力，
（2）P、D两点间的电势差．
分析：（1）分析小球到达C点的受力，根据牛顿第二定律求解加速度和细杆对小球的作用力，由牛顿第三定律得到细杆受到的压力．
（2）D、C位于同一等势面上，PD间和PC间的电势差相等．根据动能定理求出P、C间电势差，即可得到P、D两点间的电势差．
（2）D、C位于同一等势面上，PD间和PC间的电势差相等．根据动能定理求出P、C间电势差，即可得到P、D两点间的电势差．
解答：解：（1）小球到达C点时受到重力mg、Q的库仑力F和细杆的支持力N，根据牛顿第二定律得：
mg+Fcos60°=ma
N=Fsin60°
又 F=k
联立解得：a=g+
，N=
根据牛顿第三定律得：细杆所受的压力N′=N=
（2）小球从P到C过程，根据动能定理得：-qUPC+mgh=
mvC2
又由题：vC=
得：UPC=-
因为D、C位于同一等势面上，则UPD=UPC=-
．
答：
（1）小球到达C点时的加速度大小为a=g+
，细杆所受的压力为
．
（2）P、D两点间的电势差为-
．
mg+Fcos60°=ma
N=Fsin60°
又 F=k
| r2 |
联立解得：a=g+
| kQq |
| 2r2m |
| ||
| 2r2 |
根据牛顿第三定律得：细杆所受的压力N′=N=
| ||
| 2r2 |
（2）小球从P到C过程，根据动能定理得：-qUPC+mgh=
| 1 |
| 2 |
又由题：vC=
| 3gh |
得：UPC=-
| mgh |
| 2q |
因为D、C位于同一等势面上，则UPD=UPC=-
| mgh |
| 2q |
答：
（1）小球到达C点时的加速度大小为a=g+
| kQq |
| 2r2m |
| ||
| 2r2 |
（2）P、D两点间的电势差为-
| mgh |
| 2q |
点评：电势差是表示电场的能的性质的物理量，与电场力做功有关，常常应用动能定理求解电势差．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
（2009?虹口区二模）如图所示，竖直固定的光滑绝缘的直圆筒底部放置一场源A，其电荷量Q=+4×10-3 C，场源电荷A形成的电场中各点的电势表达式为
如图所示，竖直固定的木杆上穿一个小球，小球质量为m，现用恒定拉力F斜向上拉小球，恰好使小球向上做匀速运动，其中力F与杆的夹角为θ，设球与杆间的摩擦力大小为Ff，杆对球的支持力大小为FN．关于这个平衡问题，下面列出了几个平衡方程，其中正确的是（取竖直向上和水平向右为正方向）（ ）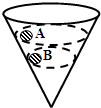
（2011?湖南模拟）如图所示，竖直固定的锥形漏斗内壁是光滑的，内壁上有两个质量相等的小球A和B，在各自不同的水平面内做匀速圆周运动．以下关于A、B两球作圆周运动时的速度（VA、VB）、角速度（ωA、ωB）、加速度（aA、aB）和对锥壁的压力（NA、NB）的说法正确的是（ ）
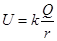，其中k为静电力恒量，r为空间某点到A的距离．有一个质量为
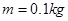的带正电小球B，B球与A球间的距离为a = 0.4 m，此时小球B处于平衡状态，且小球B在场源A形成的电场中具有的电势能表达式为
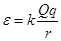，其中r为q与Q之间的距离．有一质量也为m的不带电绝缘小球C从距离B的上方H = 0.8 m处自由下落，落在小球B上立刻与小球B粘在一起向下运动，它们到达最低点后又向上运动，它们向上运动到达的最高点P．（取
，
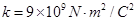），求：