题目内容
 (2009?虹口区二模)如图所示,竖直固定的光滑绝缘的直圆筒底部放置一场源A,其电荷量Q=+4×10-3 C,场源电荷A形成的电场中各点的电势表达式为U=k
(2009?虹口区二模)如图所示,竖直固定的光滑绝缘的直圆筒底部放置一场源A,其电荷量Q=+4×10-3 C,场源电荷A形成的电场中各点的电势表达式为U=k| Q |
| r |
| r |
(1)小球C与小球B碰撞后的速度为多少?
(2)小球B的带电量q为多少?
(3)P点与小球A之间的距离为多大?
(4)当小球B和C一起向下运动与场源A距离多远时,其速度最大?速度的最大值为多少?
分析:(1)根据自由下落的公式求出下落H距离的速度,由动量守恒定律求得C与小球B碰撞后的速度
(2)小球B在碰撞前处于平衡状态,根据平衡条件求解小球B的带电量
(3)C和B向下运动到最低点后又向上运动到P点,运动过程中系统能量守恒和能量守恒,列出等式求解
(4)对C和B整体进行受力分析,由能量守恒列出等式求解.
(2)小球B在碰撞前处于平衡状态,根据平衡条件求解小球B的带电量
(3)C和B向下运动到最低点后又向上运动到P点,运动过程中系统能量守恒和能量守恒,列出等式求解
(4)对C和B整体进行受力分析,由能量守恒列出等式求解.
解答:解:(1)小球C自由下落H距离的速度v0=
=4 m/s
小球C与小球B发生碰撞,由动量守恒定律得:mv0=2mv1,
所以v1=2 m/s
(2)小球B在碰撞前处于平衡状态,
对B球进行受力分析知:mg=k
,
代入数据得:q=
×10-8C
(3)C和B向下运动到最低点后又向上运动到P点,运动过程中系统能量守恒,
设P与A之间的距离为x,
由能量守恒得:
×2mv12+k
=2mg(x-a)+k
代入数据得:x=(0.4+
) m(或x=0.683 m)
(4)当C和B向下运动的速度最大时,与A之间的距离为y,
对C和B整体进行受力分析有:2mg=k
,
代入数据有:y=
m(或y=0.283 m)
由能量守恒得:
×2mv12+k
=
×2mvm2-2mg(a-y)+k
代入数据得:vm=
m/s(或vm=2.16 m/s)
答:(1)小球C与小球B碰撞后的速度为2 m/s
(2)小球B的带电量q为
×10-8C
(3)P点与小球A之间的距离为(0.4+
) m
(4)当小球B和C一起向下运动与场源A距离是
m,速度最大.其速度最大是
m/s.
| 2gH |
小球C与小球B发生碰撞,由动量守恒定律得:mv0=2mv1,
所以v1=2 m/s
(2)小球B在碰撞前处于平衡状态,
对B球进行受力分析知:mg=k
| a2 |
代入数据得:q=
| 4 |
| 9 |
(3)C和B向下运动到最低点后又向上运动到P点,运动过程中系统能量守恒,
设P与A之间的距离为x,
由能量守恒得:
| 1 |
| 2 |
| a |
| x |
代入数据得:x=(0.4+
| ||
| 5 |
(4)当C和B向下运动的速度最大时,与A之间的距离为y,
对C和B整体进行受力分析有:2mg=k
| y2 |
代入数据有:y=
| ||
| 5 |
由能量守恒得:
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| y |
代入数据得:vm=
16-8
|
答:(1)小球C与小球B碰撞后的速度为2 m/s
(2)小球B的带电量q为
| 4 |
| 9 |
(3)P点与小球A之间的距离为(0.4+
| ||
| 5 |
(4)当小球B和C一起向下运动与场源A距离是
| ||
| 5 |
16-8
|
点评:本题考察了运动学公式,平衡条件,系统能量守恒和能量守恒,要分析物体的运动过程,合理的选择物理规律.

练习册系列答案
相关题目
 (2009?虹口区二模)特种兵过山谷的一种方法可简化为图示情景.将一根长为2d的不可伸长的细绳两端固定在相距为d的.A、B两等高点,绳上挂一小滑轮P.战士们相互配合,就可沿着绳子滑到对面.如图所示,战士甲用水平力F拉住滑轮,质量为m的战士乙吊在滑轮上,脚离地,处于静止状态,此时AP竖直.然后战士甲将滑轮从静止状态释放,若不计滑轮摩擦及空气阻力,也不计滑轮的质量,求:
(2009?虹口区二模)特种兵过山谷的一种方法可简化为图示情景.将一根长为2d的不可伸长的细绳两端固定在相距为d的.A、B两等高点,绳上挂一小滑轮P.战士们相互配合,就可沿着绳子滑到对面.如图所示,战士甲用水平力F拉住滑轮,质量为m的战士乙吊在滑轮上,脚离地,处于静止状态,此时AP竖直.然后战士甲将滑轮从静止状态释放,若不计滑轮摩擦及空气阻力,也不计滑轮的质量,求:
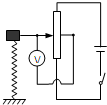 (2009?虹口区二模)一中学生为“神州七号”载人飞船设计了一个可测定竖直方向加速度的装置,其原理可简化如图,连接在竖直弹簧上的重物与滑动变阻器的滑动头连接,该装置在地面上静止时其电压表的指针指在表盘中央的零刻度处,在零刻度的两侧分别标上对应的正、负加速度值.关于这个装置在“神州七号”载人飞船发射、运行和回收过程中示数的判断正确的为 ( )
(2009?虹口区二模)一中学生为“神州七号”载人飞船设计了一个可测定竖直方向加速度的装置,其原理可简化如图,连接在竖直弹簧上的重物与滑动变阻器的滑动头连接,该装置在地面上静止时其电压表的指针指在表盘中央的零刻度处,在零刻度的两侧分别标上对应的正、负加速度值.关于这个装置在“神州七号”载人飞船发射、运行和回收过程中示数的判断正确的为 ( ) (2009?虹口区二模)如图所示,质量为m的物体带正电Q在斜面上处于静止状态,物体与斜面均在匀强电场内,匀强电场E方向水平向右.当斜面的倾角θ逐渐增大(θ<90°),而该带电体仍静止在斜面上时,则( )
(2009?虹口区二模)如图所示,质量为m的物体带正电Q在斜面上处于静止状态,物体与斜面均在匀强电场内,匀强电场E方向水平向右.当斜面的倾角θ逐渐增大(θ<90°),而该带电体仍静止在斜面上时,则( )