��Ŀ����
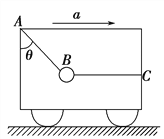
����Ŀ������ͼ��ʾ��ľ������б���ֺ�ˮƽ������ɣ�������֮����һ��Բ���������ӣ���ľ����м���λ����ֱ���ڵĹ⻬Բ�۹����б������Ϊ��.����10��������Ϊm���뾶��Ϊr�ľ��ȸ�������ʩ����1�����ˮƽ����F�������¾���ֹ����F��Բ����ͬһ��ֱ���ڣ���ʱ1�������ľ�����ˮƽ���˶�ʱ�����ĸ߶Ȳ�Ϊh.�ֳ�ȥ��FʹС��ʼ�˶���ֱ������С����˶���ˮƽ���ڣ��������ٶ�Ϊg.��

(1)ˮƽ����F�Ĵ�С��
(2)1������˶���ˮƽ��ʱ���ٶȣ�
(3)�����˶������У�2�����1���������Ĺ���
���𰸡�(1)10mgtan �� (2) ![]() (3)9mgrsin ��
(3)9mgrsin ��
�������������������1����10��С������Ϊ�о���������ƽ�⣬����ƽ���������ˮƽ����F�Ĵ�С��
��2����1����Ϊ�о������»�������ֻ���������������е���غ㣬������1������˶���ˮƽ��ʱ���ٶȣ�
��3��������Ϊ�о�����������������ˮƽ����ʱ���ٶȣ��ٶ�1�������ö��ܶ������2�����1���������Ĺ���
�⣺��1����10��С������Ϊ�о�����������ƽ�������ɵ�
Fcos��=10mgsin����
��F=10mgtan��
��2����1����Ϊ�о������ݻ�е���غ㶨�ɿɵ�
mgh=![]() ��v=
��v=![]()
��3����ȥˮƽ����F����10��С������Ϊ�о��������û�е���غ㶨�ɿɵ�
10mg��h+![]() ��=
��=![]()
�� v=![]()
��1����Ϊ�о������ɶ��ܶ�����
mgh+W=![]()
��W=9mgrsin��
�𣺣�1��ˮƽ����F�Ĵ�С��10mgtan����
��2��1������˶���ˮƽ��ʱ���ٶ���![]() ��
��
��3�������˶������У�2�����1���������Ĺ�Ϊ9mgrsin����

 ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д� С�����ϵ�д�
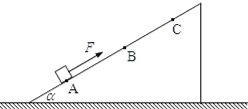
С�����ϵ�д�����Ŀ����ͼ��ʾ��һ���Ϊ37���б��̶���ˮƽ�����ϣ�����m=1kg��������ƽ����б�����ϵĺ���F�����£���A���ɾ�ֹ��ʼ�˶�������B��ʱ������ȥ����F���˺����嵽��C��ʱ�ٶ�Ϊ�㣮ÿ��0.2sͨ���ٶȴ�������������˲ʱ�ٶȣ��±������˲��ֲ������ݣ���ȡ sin37��=0.6��cos37��=0.8������
t/s | 0.0 | 0.2 | 0.4 | �� | 2.2 | 2.4 | �� |
v/ms��1 | 0.0 | 1.0 | 2.0 | �� | 3.3 | 1.2 | �� |
��1��б���Ħ��ϵ���̣�
��2������F�Ĵ�С��
��3��t=1.6sʱ�����˲ʱ�ٶȣ�