��Ŀ����
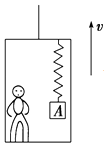
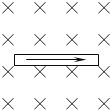
����Ŀ����ͼ��ʾ�������ȸ߹⻬�� ![]() Բ��������뾶Ϊr�����ΪL��������費�ƣ��ڹ����������һ��ֵΪR�ĵ��裬����װ�ô���һ��ֱ���ϵ���ǿ�ų��У��Ÿ�Ӧǿ��ΪB������һ�������Դ���L������Ϊm�����費�ƵĽ������ӹ���Ķ���ab���ɾ�ֹ��ʼ�»�����������cdʱ�ܵ������֧����Ϊ2mg�����������н������뵼���Ӵ����ã���
Բ��������뾶Ϊr�����ΪL��������費�ƣ��ڹ����������һ��ֵΪR�ĵ��裬����װ�ô���һ��ֱ���ϵ���ǿ�ų��У��Ÿ�Ӧǿ��ΪB������һ�������Դ���L������Ϊm�����費�ƵĽ������ӹ���Ķ���ab���ɾ�ֹ��ʼ�»�����������cdʱ�ܵ������֧����Ϊ2mg�����������н������뵼���Ӵ����ã���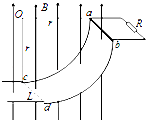
��1����������͵�ʱ���ٶȴ�С��ͨ������R�ĵ�����
��2������ab�»���cd�����л�·�в����Ľ����Ⱥ�ͨ��R�ĵ������
��3�����������������£���cd��ʼ���ٶ�v0�����ع��������Բ���˶�����ab
����д�������˶������в�����˲ʱ��Ӧ�綯����ʱ��t�ı仯��ϵ��
���ڸ˵���ab�Ĺ������������Ĺ�Ϊ���٣�
���𰸡�
��1��
�⣺������͵㣬����ţ�ٵڶ����ɵ�
N��mg=m ![]()
����� N=2mg
�ɵ� v= ![]()
��������͵�ʱ�����ĸ�Ӧ�綯��Ϊ E=BLv=BL ![]()
ͨ������R�ĵ��� I= ![]() =
= ![]()
![]()
��2��
�⣺����������ϵͳ�����غ�ã�
��·�в����Ľ����� Q=mgr�� ![]() =
= ![]() mgr
mgr
���ݷ����ڵ�Ÿ�Ӧ���ɵã�
![]() =
= ![]()
��Ӧ������ƽ��ֵ ![]() =
= ![]()
ͨ��R�ĵ���� q= ![]() ��t
��t
������ q= ![]()
�֡���=BLr
���Կɵ� q= ![]()
��3��
�⣺�ٽ��������˶�������ˮƽ����ķ��ٶ� vx=v0cos��t
�� v0=��r
�������и�Ÿ��߲��������ҽ���磺e=BLvx=BLv0cos ![]()
���ķ�֮һ�����ڣ���������Чֵ��I= ![]()
�������غ�ã��������Ĺ� W=mgr+Q
�ɽ������ɵ� Q=I2R ![]()
T= ![]()
��ã�W=mgr+ ![]()
����������1����������cd��ʱ�����������֧�����ĺ����ṩ������������ţ�ٵڶ����������������͵�ʱ���ٶȣ���E=BLv�����Ӧ�綯�ƣ�����ŷķ������ͨ��R�ĵ�������2�����������غ㶨�����·�в����Ľ����ȣ����ݷ����ڵ�Ÿ�Ӧ���ɡ�ŷķ���ɺ͵�����ʽ�Ƶ�����������ʽq= ![]() ������ͨ��R�ĵ��������3���ٰ��ع��������Բ���˶���������������˶�������ˮƽ����ķ��ٶ�vx �� ����E=BLvx��˲ʱ��Ӧ�綯�ƣ�
������ͨ��R�ĵ��������3���ٰ��ع��������Բ���˶���������������˶�������ˮƽ����ķ��ٶ�vx �� ����E=BLvx��˲ʱ��Ӧ�綯�ƣ�
�ڽ������и�Ÿ��߲������ҽ���磬���Ӧ�綯�Ƶ���Чֵ�����ɹ��ܹ�ϵ���������Ĺ���
�����㾫����������Ĺؼ��������⽹�����ɵ����֪ʶ�����ս�������:Q=I2Rt��ʽ��Q��ʾ����ͨ�������������������λ��J.�������������ǶԴ������·���ǶԷǴ������·�������õģ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�