题目内容
4.人类实现登月梦想,是从测算地月质检的距离开始;我国成功发射的“嫦娥三号”探测器,完美着陆月球虹湾地区.已知地球半径为R,地球表面重力加速度为g,月球表面的重力加速度为$\frac{1}{6}$g,月球半径为R′,月球绕地球运动的周期为T,引力常量为G,不计地球,月球自传的影响,求:(1)地月之间的距离为多少?
(2)月球的质量为多少?
分析 (1)月球绕地球做圆周运动,万有引力提供向心力,由牛顿第二定律可以求出地月间的距离.
(2)万有引力等于重力,应用万有引力公式可以求出月球的质量.
解答 解:(1)地球表面的物体受到的重力等于万有引力,即:G$\frac{Mm}{{R}^{2}}$=mg,
月球绕地球做圆周运动,万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm′}{{r}^{2}}$=m′$(\frac{2π}{T})^{2}$r,
解得:r=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$,地月间的距离:h=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R;
(2)月球表面的物体受到的重力等于万有引力,即:G$\frac{Mm}{R{′}^{2}}$=m×$\frac{1}{6}$g,
解得月球质量:M=$\frac{gR{′}^{2}}{6G}$;
答:(1)地月之间的距离为$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R;
(2)月球的质量为$\frac{gR{′}^{2}}{6G}$.
点评 本题考查了万有引力定律的应用,知道万有引力等于重力、万有引力提供向心力,应用万有引力公式与牛顿第二定律可以解题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
14. 如图甲所示,线圈ABCD固定于匀强磁场中,磁场方向垂直纸面向里,当磁感应强度如图乙所示变化时,下列说法正确的是( )
如图甲所示,线圈ABCD固定于匀强磁场中,磁场方向垂直纸面向里,当磁感应强度如图乙所示变化时,下列说法正确的是( )
 如图甲所示,线圈ABCD固定于匀强磁场中,磁场方向垂直纸面向里,当磁感应强度如图乙所示变化时,下列说法正确的是( )
如图甲所示,线圈ABCD固定于匀强磁场中,磁场方向垂直纸面向里,当磁感应强度如图乙所示变化时,下列说法正确的是( )| A. | AB边所受安培力方向向左 | B. | AB边所受安培力方向向右 | ||
| C. | 边所受安培力大小可能不变 | D. | 边所受安培力大小一定变大 |
12.以初速度v0水平抛出一物体,当其竖直位移与水平位移相等时( )
| A. | 水平分速度大小等于竖直分速度大小 | |
| B. | 运动时间为$\frac{2{v}_{0}}{g}$ | |
| C. | 物体的竖直分位移为$\frac{{{v}_{0}}^{2}}{g}$ | |
| D. | 物体的水平分位移为$\frac{{{v}_{0}}^{2}}{2g}$ |
19. 如图所示,一小车在水平面上以加速度a向右做加速运动,在车内的光滑竖直壁和光滑斜面之间有一质量为m的小球,当加速度增大时,下列说法正确的是( )
如图所示,一小车在水平面上以加速度a向右做加速运动,在车内的光滑竖直壁和光滑斜面之间有一质量为m的小球,当加速度增大时,下列说法正确的是( )
 如图所示,一小车在水平面上以加速度a向右做加速运动,在车内的光滑竖直壁和光滑斜面之间有一质量为m的小球,当加速度增大时,下列说法正确的是( )
如图所示,一小车在水平面上以加速度a向右做加速运动,在车内的光滑竖直壁和光滑斜面之间有一质量为m的小球,当加速度增大时,下列说法正确的是( )| A. | 竖直壁对小球的弹力增大,斜面对小球的弹力减小 | |
| B. | 竖直壁对小球的弹力不变,斜面对小球的弹力减小 | |
| C. | 竖直壁对小球的弹力增大,斜面对小球的弹力不变 | |
| D. | 竖直壁对小球的弹力减小,斜面对小球的弹力不变 |
6.下列说法正确的是( )
| A. | 研究地球公转时,由于地球很大,所以不能将地球看做质点 | |
| B. | 在某段时间内,运动质点的位移一定不为零 | |
| C. | 受到弹力作用的物体一定受摩擦力作用 | |
| D. | 摩擦力的方向不一定与物体运动方向相反 |
4.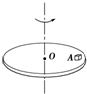 如图所示,小物体A与水平圆盘保持相对静止,随圆盘一起做匀速圆周运动,则关于A的受力情况,下列说法正确的是( )
如图所示,小物体A与水平圆盘保持相对静止,随圆盘一起做匀速圆周运动,则关于A的受力情况,下列说法正确的是( )
 如图所示,小物体A与水平圆盘保持相对静止,随圆盘一起做匀速圆周运动,则关于A的受力情况,下列说法正确的是( )
如图所示,小物体A与水平圆盘保持相对静止,随圆盘一起做匀速圆周运动,则关于A的受力情况,下列说法正确的是( )| A. | 只受重力、支持力 | B. | 只受向心力、摩擦力 | ||
| C. | 受重力、支持力、向心力、摩擦力 | D. | 受重力、支持力、摩擦力 |
 如图所示,将质量为3kg的小球水平抛出,空气阻力不计,求:
如图所示,将质量为3kg的小球水平抛出,空气阻力不计,求: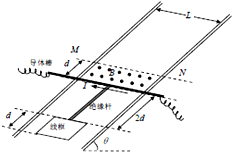 如图所示,两足够长的平等光滑金属导轨安装在一倾角为θ的光滑绝缘斜面上,导轨间距为L,电阻忽略不计,一宽度为d的有界匀强磁场垂直于斜面向上,磁感应强度为B,另有一长为2d的绝缘杆将一导体棒和一边长为d(d<L)的正方形导线框连在一起组成固定装置.总质量为m,导体棒中通有大小恒温I的电流,将该装置置于导轨上,开始时导体棒恰好位于磁场的下边界处,由静止释放后装置沿斜面向上运动,当线框的下边运动到磁场的上边界MN处时装置的速度恰好为零.重力加速度大小为g.
如图所示,两足够长的平等光滑金属导轨安装在一倾角为θ的光滑绝缘斜面上,导轨间距为L,电阻忽略不计,一宽度为d的有界匀强磁场垂直于斜面向上,磁感应强度为B,另有一长为2d的绝缘杆将一导体棒和一边长为d(d<L)的正方形导线框连在一起组成固定装置.总质量为m,导体棒中通有大小恒温I的电流,将该装置置于导轨上,开始时导体棒恰好位于磁场的下边界处,由静止释放后装置沿斜面向上运动,当线框的下边运动到磁场的上边界MN处时装置的速度恰好为零.重力加速度大小为g.