题目内容
3.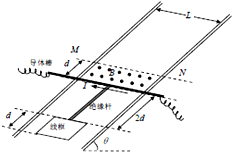 如图所示,两足够长的平等光滑金属导轨安装在一倾角为θ的光滑绝缘斜面上,导轨间距为L,电阻忽略不计,一宽度为d的有界匀强磁场垂直于斜面向上,磁感应强度为B,另有一长为2d的绝缘杆将一导体棒和一边长为d(d<L)的正方形导线框连在一起组成固定装置.总质量为m,导体棒中通有大小恒温I的电流,将该装置置于导轨上,开始时导体棒恰好位于磁场的下边界处,由静止释放后装置沿斜面向上运动,当线框的下边运动到磁场的上边界MN处时装置的速度恰好为零.重力加速度大小为g.
如图所示,两足够长的平等光滑金属导轨安装在一倾角为θ的光滑绝缘斜面上,导轨间距为L,电阻忽略不计,一宽度为d的有界匀强磁场垂直于斜面向上,磁感应强度为B,另有一长为2d的绝缘杆将一导体棒和一边长为d(d<L)的正方形导线框连在一起组成固定装置.总质量为m,导体棒中通有大小恒温I的电流,将该装置置于导轨上,开始时导体棒恰好位于磁场的下边界处,由静止释放后装置沿斜面向上运动,当线框的下边运动到磁场的上边界MN处时装置的速度恰好为零.重力加速度大小为g.(1)求刚释放时装置加速度的大小;
(2)求上述运动过程中线框中产生的热量;
(3)装置速度为零后将向下运动,然后再向上运动,经过若干次往返,最终装置将在斜面上做稳定的往复运动,求稳定后装置运动的最高位置与最低位置之间的距离.
分析 (1)根据装置的受力情况,由牛顿第二定律求加速度的大小.
(2)在运动过程中装置的动能变化量为零,根据动能定理求出克服安培力做功,即可得到产生的热量.
(3)稳定后,装置运动到最高位置与最低位置的速度,由动能定理可求得最低位置时金属棒距离上边界的距离.装置往复运动的最高位置:线框的上边位于磁场的下边界,此时导体棒距磁场上边界d,可得装置运动的最高位置与最低位置之间的距离为x+d.
解答 解:(1)刚释放时,根据牛顿第二定律得 ma=BIL-mgsinθ
可得加速度大小为 a=$\frac{BIL}{M}$-gsinθ
(2)设装置由静止释放到线框的下边运动到磁场的上边界MN的过程中,安培力对线框做功的大小为W,根据动能定理有:
0-0=BILd-mgsinθ•4d-W
解得 W=BILd-4mgdsinθ
线框中产生的热量 Q=W=BILd-4mgdsinθ
(3)装置往复运动的最高位置:线框的上边位于磁场的下边界,此时导体棒距磁场上边界d;
往复运动到最低位置时,金属棒在磁场内,设距离上边界为x,则功能关系得
mgsinθ•(x+d)=BIL•x
可解出x=$\frac{mgdsinθ}{BIL-mgsinθ}$
装置运动的最高位置与最低位置之间的距离为
x+d=$\frac{mgdsinθ}{BIL-mgsinθ}$+d=$\frac{BILd}{BIL-mgsinθ}$
答:(1)刚释放时装置加速度的大小是$\frac{BIL}{M}$-gsinθ;
(2)上述运动过程中线框中产生的热量是BILd-4mgdsinθ.
(3)装置运动的最高位置与最低位置之间的距离为$\frac{BILd}{BIL-mgsinθ}$.
点评 当线框产生感应电流时,由安培力做功从而产生热量.因安培力不恒定,所以运用动能定理求安培力做功从而得产生的热量,也可利用能量守恒定律解题.

 阅读快车系列答案
阅读快车系列答案 如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )
如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )| A. | F1=$\frac{G}{sinα}$ | |
| B. | F2=$\frac{G}{sinα}$ | |
| C. | 若缓慢减小绳索的长度,F1与F2的合力变大 | |
| D. | 若缓慢减小绳索的长度,F1与F2都增大 |
 一个小球在细绳的拉力作用下,绕某固定点在竖直平面内作圆周运动,空气阻力不计.小球在运动过程中不发生改变的物理是( )
一个小球在细绳的拉力作用下,绕某固定点在竖直平面内作圆周运动,空气阻力不计.小球在运动过程中不发生改变的物理是( )| A. | 速度 | B. | 加速度 | C. | 向心力 | D. | 机械能 |
 世界上最大的太阳能飞机“阳光动力”2号于2015年3月31日凌晨抵达重庆江北国际机场,正式开启中国旅程,飞机的机翼上,镶嵌了17000片太阳能电池,为飞机上四个电动马达提供电力,实现零燃料飞行.关于能源和能量,下列说法中正确的是( )
世界上最大的太阳能飞机“阳光动力”2号于2015年3月31日凌晨抵达重庆江北国际机场,正式开启中国旅程,飞机的机翼上,镶嵌了17000片太阳能电池,为飞机上四个电动马达提供电力,实现零燃料飞行.关于能源和能量,下列说法中正确的是( )| A. | 人类对太阳能的利用,说明能量可以创生 | |
| B. | 能量消耗说明自然界的能量在不断减少 | |
| C. | 自然界的能量不会消灭,所以不需要节约能源 | |
| D. | 人类应多开发与利用太阳能、风能等新能源 |
 如图所示,间距为d的平行、光滑金属导轨,垂直放置在磁感应强度大小为B的匀强磁场中.质量为m的导体棒ab垂直于导轨放置,且与两导轨保持良好接触,现导体棒以初速度v0进入磁场,运动一段距离后速度为零.则此过程( )
如图所示,间距为d的平行、光滑金属导轨,垂直放置在磁感应强度大小为B的匀强磁场中.质量为m的导体棒ab垂直于导轨放置,且与两导轨保持良好接触,现导体棒以初速度v0进入磁场,运动一段距离后速度为零.则此过程( )| A. | 导体棒做匀减速运动 | |
| B. | 导体棒上感应电流方向由a向b | |
| C. | 导体棒刚进入磁场时感应电动势大小为Bdv0 | |
| D. | 运动过程中回路中产生的焦耳热为$\frac{1}{2}$mv02 |
 如图所示,一小物块以大小为v0的初速度从曲面的P点下滑,运动到Q点时速度大小仍为
如图所示,一小物块以大小为v0的初速度从曲面的P点下滑,运动到Q点时速度大小仍为v0,若小物块以大小为v(v>v0)的初速度仍由P点下滑,则小物块运动到Q点时的速度大小为( )
| A. | 大于v | B. | 等于v | ||
| C. | 小于v | D. | 条件不足,无法判断 |
 某同学利用竖直上抛小球的频闪照片“验证机械能守恒定律”.频闪仪每隔0.05s闪光一次,照片的一部分如图所示.图中所标数据为实际距离.小球的质量m=0.20kg,当地重力加速度取9.8m/s2,计算结果保留三位有效数字
某同学利用竖直上抛小球的频闪照片“验证机械能守恒定律”.频闪仪每隔0.05s闪光一次,照片的一部分如图所示.图中所标数据为实际距离.小球的质量m=0.20kg,当地重力加速度取9.8m/s2,计算结果保留三位有效数字 有一种圆珠笔,内部有一根小弹簧,如图所示,当笔杆竖直放置时,在圆珠笔尾部的按钮尾部的按钮上放一个200g的砝码,砝码静止时,弹簧压缩量为2mm,现用这支圆珠笔水平推一本放在水平桌面上质量为800g的书,当按钮压缩量为2.4mm(未超过弹簧的弹性限度)时,这本书恰好匀速运动,则笔内小弹簧的劲度系数为1000N/m,书与桌面间的动摩擦因数为0.3.
有一种圆珠笔,内部有一根小弹簧,如图所示,当笔杆竖直放置时,在圆珠笔尾部的按钮尾部的按钮上放一个200g的砝码,砝码静止时,弹簧压缩量为2mm,现用这支圆珠笔水平推一本放在水平桌面上质量为800g的书,当按钮压缩量为2.4mm(未超过弹簧的弹性限度)时,这本书恰好匀速运动,则笔内小弹簧的劲度系数为1000N/m,书与桌面间的动摩擦因数为0.3.