题目内容
9. 如图所示,将质量为3kg的小球水平抛出,空气阻力不计,求:
如图所示,将质量为3kg的小球水平抛出,空气阻力不计,求:(1)抛出时人对球所做的功;
(2)抛出后0.2s小球的动能.
分析 (1)由平抛运动规律可求得抛出时的初速度,再由动能定理可求得抛出过程所做的功;
(2)由平抛运动规律可求得0.2s内物体的竖直位移;再由机械能守恒定律可求得抛出0.2s时的动能.
解答 解:(1)由图可知,小球的竖直位移为19.6m;水平位移为40m;
则由平抛运动规律可知:
h=$\frac{1}{2}g{t}^{2}$
x=v0t
代入数据解得:v0=20m/s;
由动能定理可得:人做功为:W=$\frac{1}{2}$mv2=$\frac{1}{2}$×3×400=600J;
(2)下落0.2s时,物体下落的高度为:h=$\frac{1}{2}×9.8×0.04$=0.196m;
则对抛出过程由机械能守恒定律可得:
mgh=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02
解得:$\frac{1}{2}$mv2=600+30×0.196=605.88J;
答:(1)抛出时人对球所做的功为20m/s;
(2)抛出后0.2s小球的动能为605.88J.
点评 本题考查动能定理和机械能守恒定律的应用,要注意明确小球在抛出时为变力做功,故只能由动能定理求解功.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
19.天文学家发现某恒星有一颗行星在圆形轨道上绕其运动,并测出了行星的轨道半径R和公转周期T,已知引力常量为G,由此可算出( )
| A. | 恒星质量 | B. | 恒星平均密度 | C. | 行星质量 | D. | 行星半径 |
20.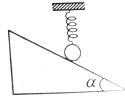 竖直弹簧的下端悬挂一小球,静止时,弹簧对小球的拉力大小为T.现使小球靠着倾角为α的光滑斜面,弹簧仍保持竖直,且整个装置处于静止状态,如图所示,则小球对斜面的压力大小为( )
竖直弹簧的下端悬挂一小球,静止时,弹簧对小球的拉力大小为T.现使小球靠着倾角为α的光滑斜面,弹簧仍保持竖直,且整个装置处于静止状态,如图所示,则小球对斜面的压力大小为( )
 竖直弹簧的下端悬挂一小球,静止时,弹簧对小球的拉力大小为T.现使小球靠着倾角为α的光滑斜面,弹簧仍保持竖直,且整个装置处于静止状态,如图所示,则小球对斜面的压力大小为( )
竖直弹簧的下端悬挂一小球,静止时,弹簧对小球的拉力大小为T.现使小球靠着倾角为α的光滑斜面,弹簧仍保持竖直,且整个装置处于静止状态,如图所示,则小球对斜面的压力大小为( )| A. | T | B. | 0 | C. | Tcosα | D. | Ttanα |
11.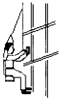 如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )
如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )
 如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )
如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )| A. | F1=$\frac{G}{sinα}$ | |
| B. | F2=$\frac{G}{sinα}$ | |
| C. | 若缓慢减小绳索的长度,F1与F2的合力变大 | |
| D. | 若缓慢减小绳索的长度,F1与F2都增大 |
8. 一个小球在细绳的拉力作用下,绕某固定点在竖直平面内作圆周运动,空气阻力不计.小球在运动过程中不发生改变的物理是( )
一个小球在细绳的拉力作用下,绕某固定点在竖直平面内作圆周运动,空气阻力不计.小球在运动过程中不发生改变的物理是( )
 一个小球在细绳的拉力作用下,绕某固定点在竖直平面内作圆周运动,空气阻力不计.小球在运动过程中不发生改变的物理是( )
一个小球在细绳的拉力作用下,绕某固定点在竖直平面内作圆周运动,空气阻力不计.小球在运动过程中不发生改变的物理是( )| A. | 速度 | B. | 加速度 | C. | 向心力 | D. | 机械能 |
9.高一某同学在校运会上参加跳高比赛,其起跳后身体横着越过横杆,则其由起跳到最高点的过程中,克服重力做的功最接近( )
| A. | 5J | B. | 50J | C. | 500J | D. | 5000J |
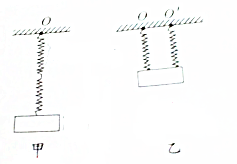 如图甲所示,用两根完全相同的弹簧连接起来悬挂一质量m=1kg的物体.若弹簧的原长l0=20 cm,劲度系数k=100 N/m,不计弹簧的质量.(取g=10 N/kg)
如图甲所示,用两根完全相同的弹簧连接起来悬挂一质量m=1kg的物体.若弹簧的原长l0=20 cm,劲度系数k=100 N/m,不计弹簧的质量.(取g=10 N/kg) 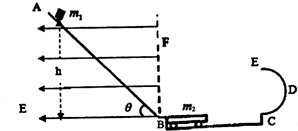 安庆市某中学物理兴趣小组设计了如图所示的轨道,AB为动摩擦因素μ1=0.25的倾斜轨道,斜面倾角θ=53°,竖直边界BF的左侧空间存在场强大小E=5×104V/m,方向水平向左的匀强磁场.底端有一小段将其转接为水平的弧形轨道(m1从斜面过渡到小车上时不考虑动能的损失),BC是一个光滑的水平凹槽,凹槽内放置一个质量为m2=$\frac{1}{3}$kg的小车,小车上表面与凹槽的两端点BC等高,CDE是光滑的半径为R=0.2m的竖直半圆形轨道,E是圆轨道的最高点.将一个质量为m1=1kg、带正电q=1.5×10-4C的小滑块(可视为质点),以初速度v0=3m/s从AB轨道上离B点高h=5.6m处开始释放,滑块下滑后从B点滑上小车,在到达C点之前,滑块与小车达到共同速度,小车与凹槽碰撞后立即停止,此后滑块继续运动,小车的长度L=1.5m.滑块与小车之间的动摩擦因数μ2=0.2,g=10m/s2.试求:
安庆市某中学物理兴趣小组设计了如图所示的轨道,AB为动摩擦因素μ1=0.25的倾斜轨道,斜面倾角θ=53°,竖直边界BF的左侧空间存在场强大小E=5×104V/m,方向水平向左的匀强磁场.底端有一小段将其转接为水平的弧形轨道(m1从斜面过渡到小车上时不考虑动能的损失),BC是一个光滑的水平凹槽,凹槽内放置一个质量为m2=$\frac{1}{3}$kg的小车,小车上表面与凹槽的两端点BC等高,CDE是光滑的半径为R=0.2m的竖直半圆形轨道,E是圆轨道的最高点.将一个质量为m1=1kg、带正电q=1.5×10-4C的小滑块(可视为质点),以初速度v0=3m/s从AB轨道上离B点高h=5.6m处开始释放,滑块下滑后从B点滑上小车,在到达C点之前,滑块与小车达到共同速度,小车与凹槽碰撞后立即停止,此后滑块继续运动,小车的长度L=1.5m.滑块与小车之间的动摩擦因数μ2=0.2,g=10m/s2.试求: