题目内容
1．
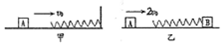如图甲所示，在光滑水平面上，轻质弹簧一端固定，物体A以速度v0向右运动压缩弹簧，测得弹簧的最大压缩量为x，现让弹簧一端连接另一质量为m的物体B（如图乙所示），物体A以2v0的速度向右压缩弹簧，测得弹簧的最大压缩量仍为x，则（ ）| A． | A物体的质量为3m | |
| B． | A物体的质量为2m | |
| C． | 弹簧压缩最大时的弹性势能为$\frac{3}{2}$mv02 | |
| D． | 弹簧压缩最大时的弹性势能为mv02 |
分析 水平面光滑，物块压缩弹簧时，物块的动能转化为弹簧的弹性势能，弹簧被压缩过程中最大的弹性势能等于物块的初动能．
A、B速度相等时，弹簧的弹性势能最大，由动量守恒定律与能量守恒定律可以求出最大弹性势能的表达式，然后求出A与B的质量之间的关系．
解答 解：当弹簧固定时，当弹簧压缩量最大时，弹性势能最大，A的动能转化为弹簧的弹性势能，根据系统的机械能守恒得：弹簧被压缩过程中最大的弹性势能等于A的初动能，设A的质量为mA，即有：
Epm=$\frac{1}{2}{m}_{A}{v}_{0}^{2}$ ①
当弹簧一端连接另一质量为m的物体B时，A与弹簧相互作用的过程中B将向右运动，A、B速度相等时，弹簧的弹性势能最大，选取A的初速度的方向为正方向，
由动量守恒定律得：mA•2v0=（m+mA）v，②
由机械能守恒定律得：△${E}_{pm}=\frac{1}{2}{m}_{A}{{（2v}_{0}^{\;}）}^{2}-\frac{1}{2}（{m}_{A}+m）{v}^{2}$，③
联立得：mA=3m ④
联立①④得：Epm=1.5mv02
故AC正确，BD错误．
故选：AC
点评 本题考查了求弹簧的弹性势能、B的速度，分析清楚物体运动过程是正确解题的前提与关键，应用动量守恒定律与机械能守恒定律即可正确解题．
练习册系列答案
相关题目
5．卫星发射时，可利用其随地球自转的速度，达到节省燃料的目的．仅从该角度考虑，卫星发射场的位置应建在（ ）
| A． | 赤道附近 | B． | 靠近南极 | C． | 靠近北极 | D． | 地面任意处 |
12．图甲是小型交流发电机的示意图，两磁极N、S间的磁场可视为水平方向的匀强磁场，
为交流电流表．线圈绕垂直于磁场的水平轴OO′沿逆时针方向匀速转动，从图甲所示位置开始计时，产生的交变电流随时间变化的图象如图乙所示．以下判断正确的是（ ）
为交流电流表．线圈绕垂直于磁场的水平轴OO′沿逆时针方向匀速转动，从图甲所示位置开始计时，产生的交变电流随时间变化的图象如图乙所示．以下判断正确的是（ ）| A． | 线圈转动的角速度为50π rad/s | |
| B． | 电流表的示数为10A | |
| C． | t=0.01s时，线圈平面与磁场方向平行 | |
| D． | t=0.02s时，电阻R中电流的方向自右向左 |
9．装有一定量液体的玻璃管竖直漂浮在水中，水面足够大，如图甲所示．把玻璃管向下缓慢按压4cm后放手，忽略运动阻力，玻璃管的运动可以视为竖直方向的简谐运动，测得振动周期为0.5s．竖直向上为正方向，某时刻开始计时，其振动图象如图乙所示，其中A为振幅．对于玻璃管，下列说法正确的是 （ ）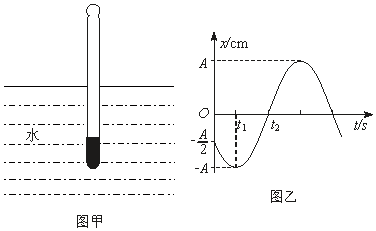
| A． | 回复力等于重力和浮力的合力 | |
| B． | 振动过程中动能和重力势能相互转化，玻璃管的机械能守恒 | |
| C． | 位移满足函数式x=4sin（4πt-$\frac{5π}{6}$）cm | |
| D． | 振动频率与按压的深度有关 | |
| E． | 在t1～t2时间内，位移减小，加速度减小，速度增大 |
16．关于机械波．电磁波和相对论的下列说法中正确的是（ ）
| A． | 机械波和电磁波在介质中的传播速度仅由介质决定 | |
| B． | 假设火车以接近光速的速度通过站台，站台上的旅客观察到车上的乘客变矮了 | |
| C． | 简谐机械波传播时单位时间内经过介质中某点的完全波的个数就是这列波的频率 | |
| D． | 用光导纤维束传播图象信息利用了光的全反射 | |
| E． | 在真空中传播的两列电磁波，频率大的波长短 |
6．某同学设计了一个既可以测电阻由可以测电动势和内阻的实验电路，如图甲所示，实验室提供了一下实验器材：
电源E（电动势为6V，内阻约为1Ω）
定值电阻R0（阻值约为5Ω）
电流表A（量程30mA，内阻约为0.5Ω）
电流表B（量程0.6A，内阻约为1Ω）
电压表C（量程8V，内阻约为5kΩ）
电压表D（量程4V，内阻约为3kΩ）
滑动变阻器F（阻值0-10Ω）
滑动变阻器G（阻值0-500Ω）
根据题中所给信息，请回答以下问题
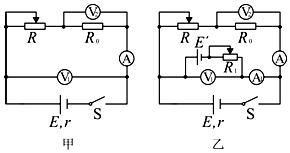
（1）电流表应选B，滑动变阻器应选F；（选填器材代号）
（2）该同学操作正确无误，用U1、U2、I分别表示电表
、
、
的读数，其数据如表所示：
根据表中数据求得定值电阻R0=4.8Ω（保留两位有效数字），其测量值＜真实值（填＞、＜或=）；该同学同时利用上表测得的数据求得电源的电动势和内阻，由误差分析可知，电动势的测量值＜电动势的真实值（填＞、＜或=）．
（3）该同学进一步利用一个辅助电源E′，采用如图乙所示的电路测量电源的电动势，测量过程中，调节R后再调节R1，使得A1的示数变为0，测得多组数据，这样，电源电动势值=电源电动势的真实值（填＞、＜或=）．
电源E（电动势为6V，内阻约为1Ω）
定值电阻R0（阻值约为5Ω）
电流表A（量程30mA，内阻约为0.5Ω）
电流表B（量程0.6A，内阻约为1Ω）
电压表C（量程8V，内阻约为5kΩ）
电压表D（量程4V，内阻约为3kΩ）
滑动变阻器F（阻值0-10Ω）
滑动变阻器G（阻值0-500Ω）
根据题中所给信息，请回答以下问题
（1）电流表应选B，滑动变阻器应选F；（选填器材代号）
（2）该同学操作正确无误，用U1、U2、I分别表示电表
、、的读数，其数据如表所示：| I（A） | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 |
| U1（V） | 5.68 | 5.61 | 5.57 | 5.51 | 5.48 | 5.40 |
| U2（V） | 1.44 | 1.69 | 1.91 | 2.16 | 2.39 | 2.62 |
（3）该同学进一步利用一个辅助电源E′，采用如图乙所示的电路测量电源的电动势，测量过程中，调节R后再调节R1，使得A1的示数变为0，测得多组数据，这样，电源电动势值=电源电动势的真实值（填＞、＜或=）．
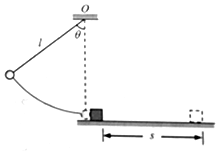如图所示，质量m1=4kg的小球用一条不可伸长的轻绳连接，绳的另一端固定在悬点O上，绳子长度l=0.5m，将小球拉至绳子偏离竖直方向的角度θ=53°处由静止释放，小球运动至最低点时，与一质量m2=2kg的物块发生正碰，碰撞时间很短，之后物块在水平面上滑行一段s=0.4m的距离后停下，已知物块与水平面见得动摩擦因数μ=0.5，取重力加速度g=10m/s2，sin53°=0.8，cos53°=0.6，求：
10．
高大建筑上都有一竖立的避雷针，用以把聚集在云层中的电荷导入大地． 在赤道某地两建筑上空，有一团带负电的乌云经过其正上方时，发生放 电现象，如图所示．则此过程中地磁场对避雷针的作用力的方向是（ ）
高大建筑上都有一竖立的避雷针，用以把聚集在云层中的电荷导入大地． 在赤道某地两建筑上空，有一团带负电的乌云经过其正上方时，发生放 电现象，如图所示．则此过程中地磁场对避雷针的作用力的方向是（ ）| A． | 向东 | B． | 向南 | C． | 向西 | D． | 向北 |
17．
如图所示，光滑斜面被分成四个长度相等的部分，即 AB=BC=CD=DE，一物体由 A 点静止释放，下列结论正确的是（ ）
如图所示，光滑斜面被分成四个长度相等的部分，即 AB=BC=CD=DE，一物体由 A 点静止释放，下列结论正确的是（ ）| A． | 物体到达各点的速率之比v B：vC：v D：vE=1：$\sqrt{2}$：$\sqrt{3}$：2 | |
| B． | 物体到达各点所经历的时间t E=2t B=$\sqrt{2}$tC=$\frac{2}{\sqrt{3}}$tD | |
| C． | 物体从 A 运动到 E 的全过程平均速度$\overline{v}$=vB | |
| D． | 物体通过每一部分时，其速度增量v B-vA=v D-vC=v E-vD |