题目内容
A.甲、乙是两颗绕地球作匀速圆周运动的人造卫星,其线速度大小之比为
:1,则这两颗卫星的运转半径之比为 ,运转周期之比为 .
B.A、B两物体在光滑水平地面上沿一直线相向而行,A质量为5kg,速度大小为10m/s,B质量为2kg,速度大小为5m/s,它们的总动量大小为 kgm/s;两者相碰后,A沿原方向运动,速度大小为4m/s,则B的速度大小为 m/s.
| 2 |
B.A、B两物体在光滑水平地面上沿一直线相向而行,A质量为5kg,速度大小为10m/s,B质量为2kg,速度大小为5m/s,它们的总动量大小为
分析:A、绕地球作匀速圆周运动的人造卫星,由地球的万有引力提供向心力,速度公式为v=
,可求出半径之比,由T=
求出周期之比.
B、取A球的速度方向为正方向,分别表示出两球的动量,即可求出总动量.碰撞过程遵守动量守恒,求出B的速度大小.
|
| 2πr |
| v |
B、取A球的速度方向为正方向,分别表示出两球的动量,即可求出总动量.碰撞过程遵守动量守恒,求出B的速度大小.
解答:解:A、绕地球作匀速圆周运动的人造卫星的速度为v=
,M是地球的质量,则这两颗卫星的运转半径之比为rA:rB=
:
=1:2.卫星的周期为T=
,则运转周期之比为TA:TB=
:
=
:4.
B、取A球的速度方向为正方向,AB的总动量大小为P=mAvA-mBvB=5×10-2×5=40(kgm/s).根据动量守恒得
P=mAvA′+mBvB′,解得,vB′=10m/s
故答案为:A、1:2,
:4.B、40,10
|
| v | 2 B |
| v | 2 A |
| 2πr |
| v |
| rA |
| vA |
| rB |
| vB |
| 2 |
B、取A球的速度方向为正方向,AB的总动量大小为P=mAvA-mBvB=5×10-2×5=40(kgm/s).根据动量守恒得
P=mAvA′+mBvB′,解得,vB′=10m/s
故答案为:A、1:2,
| 2 |
点评:对于卫星问题,掌握速度公式v=
,由圆周运动的规律可推导出角速度、周期、向心加速度等表达式;对于碰撞的基本规律是动量守恒,要熟悉.
|

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
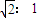 ,则这两颗卫星的运转半径之比为 ,运转周期之比为 .
,则这两颗卫星的运转半径之比为 ,运转周期之比为 .