题目内容
9.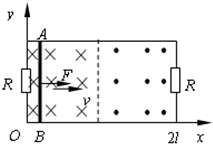 矩形裸导线框长边的长度为2l,短边的长度为l,在两个短边上均接有阻值为R的电阻,其余部分电阻均不计.导线框的位置如图所示,线框内的磁场方向及分布情况如图,大小为$B={B_0}cos({\frac{πx}{2l}})$.一电阻为R的光滑导体棒AB与短边平行且与长边始终接触良好.起初导体棒处于x=0处,从t=0时刻起,导体棒AB在沿x方向的外力F的作用下做速度为v的匀速运动.试求:
矩形裸导线框长边的长度为2l,短边的长度为l,在两个短边上均接有阻值为R的电阻,其余部分电阻均不计.导线框的位置如图所示,线框内的磁场方向及分布情况如图,大小为$B={B_0}cos({\frac{πx}{2l}})$.一电阻为R的光滑导体棒AB与短边平行且与长边始终接触良好.起初导体棒处于x=0处,从t=0时刻起,导体棒AB在沿x方向的外力F的作用下做速度为v的匀速运动.试求:(1)导体棒AB两端的感应电动势随时间的变化规律;
(2)导体棒AB从x=0运动到x=2l的过程中外力F随时间t变化的规律;
(3)导体棒AB从x=0运动到x=2l的过程中整个回路产生的热量.
分析 (1)导体棒匀速运动,其坐标为x=vt,由e=Blv求出导体棒产生的感应电动势,
(2)根据闭合电路欧姆定律求出 通过AB棒的感应电流i,由F安=Bil求安培力,即可由平衡条件求得外力与t关系的表达式;
(3)导体棒AB在切割磁感线的过程中产生半个周期的正弦交流电,由感应电动势的瞬时表达式,求出感应电动势的有效值,由焦耳定律求出热量.
解答 解:(1)在t时刻AB棒的坐标为:x=vt
感应电动势:$e=Blv={B_0}lvcos\frac{πvt}{2l}$
(2)回路总电阻:R总=R+$\frac{1}{2}$R=$\frac{3}{2}$R
回路感应电流:i=$\frac{e}{{R}_{总}}$=$\frac{2{B}_{0}lvcos\frac{πvt}{2l}}{3R}$
棒匀速运动时有:F=F安=BIl
解得:$F=\frac{{2B_0^2{l^2}v{{cos}^2}(\frac{πvt}{2l})}}{3R}$$(0≤t≤\frac{2l}{v})$
(3)导体棒AB在切割磁感线的过程中产生半个周期的正弦交流电,
感应电动势的有效值为:$E=\frac{{\sqrt{2}}}{2}{B_0}lv$
回路产生的电热:Q=$\frac{{E}^{2}}{{R}_{总}}$t
通电时间t=$\frac{2l}{v}$
联立解得Q=$\frac{2{{B}_{0}}^{2}{l}^{3}v}{3R}$
答:(1)某一时刻t产生的电动势e=B0lvcos$\frac{πvt}{2l}$;
(2)某一时刻t所受的外力$F=\frac{{2B_0^2{l^2}v{{cos}^2}(\frac{πvt}{2l})}}{3R}$$(0≤t≤\frac{2l}{v})$;
(3)整个回路产生的热量Q=$\frac{2{{B}_{0}}^{2}{l}^{3}v}{3R}$.
点评 本题以正弦式电流的产生来考查电磁感应的应用;关键要掌握电磁感应和电路的基本规律,知道在计算热量时一定要用到有效值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案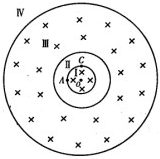 如图所示,三个半径分别为R,2R,6R的同心圆将空间分为Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域,其中圆形区域Ⅰ和环形区域Ⅲ内有垂直纸面向里的匀强磁场,磁感应强度分别为B和$\frac{B}{2}$,一个质子从区域Ⅰ边界上的A点以速度v沿半径方向射入磁场,经磁场偏转恰好从区域Ⅰ边界上的C点飞出,AO垂直CO,则关于质子的运动,下列说法正确的是( )
如图所示,三个半径分别为R,2R,6R的同心圆将空间分为Ⅰ,Ⅱ,Ⅲ,Ⅳ四个区域,其中圆形区域Ⅰ和环形区域Ⅲ内有垂直纸面向里的匀强磁场,磁感应强度分别为B和$\frac{B}{2}$,一个质子从区域Ⅰ边界上的A点以速度v沿半径方向射入磁场,经磁场偏转恰好从区域Ⅰ边界上的C点飞出,AO垂直CO,则关于质子的运动,下列说法正确的是( )| A. | 质子最终将离开区域Ⅲ在区域Ⅳ匀速运动 | |
| B. | 质子最终将一直在区域Ⅲ内做匀速圆周运动 | |
| C. | 质子能够回到初始点A,且周而复始的运动 | |
| D. | 质子能够回到初始点A,且回到初始点前,在区域Ⅲ中运动的时间是在区域Ⅰ中运动时间的6倍 |
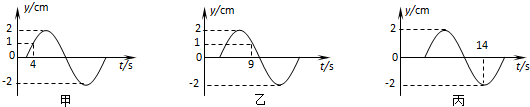
| A. | 该波的波长为6m | |
| B. | 该波的周期为12s | |
| C. | 该波的波速为1m/s | |
| D. | 10s末A点的振动速度大于B点的振动速度 |
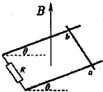 处于竖直向上匀强磁场中的两根电阻不计的平行金属导轨,下端连一电阻R,导轨与水平面之间的夹角为θ.一电阻可忽略的金属棒ab,开始固定在两导轨上某位置,棒与导轨垂直,如图所示.现释放金属棒让其由静止开始沿轨道平面下滑.就导轨光滑和粗糙两种情况相比较,当两次下滑的位移相同时( )
处于竖直向上匀强磁场中的两根电阻不计的平行金属导轨,下端连一电阻R,导轨与水平面之间的夹角为θ.一电阻可忽略的金属棒ab,开始固定在两导轨上某位置,棒与导轨垂直,如图所示.现释放金属棒让其由静止开始沿轨道平面下滑.就导轨光滑和粗糙两种情况相比较,当两次下滑的位移相同时( )| A. | 金属棒的动能相同 | B. | 金属棒的机械能变化量相同 | ||
| C. | 流过R的电量相等 | D. | 闭合回路中磁通量的变化率相等 |
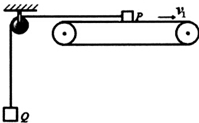 如图所示,水平传送带在电动机带动下以速度v1=2m/s匀速运动,小物体P、Q质量分别为0.2kg和0.3kg,由通过定滑轮且不可伸长的轻绳相连,t=O时刻P放在传送带中点处由静止释放.已知P与传送带间的动摩擦因数为O.5,传送带水平部分两端点间的距离为4m,不计定滑轮质量及摩擦,P与定滑轮间的绳水平,取g=1Om/s2.
如图所示,水平传送带在电动机带动下以速度v1=2m/s匀速运动,小物体P、Q质量分别为0.2kg和0.3kg,由通过定滑轮且不可伸长的轻绳相连,t=O时刻P放在传送带中点处由静止释放.已知P与传送带间的动摩擦因数为O.5,传送带水平部分两端点间的距离为4m,不计定滑轮质量及摩擦,P与定滑轮间的绳水平,取g=1Om/s2. 如图所示,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平导轨上,弹簧处在原长状态.滑块A从半径为R的光滑$\frac{1}{4}$圆弧槽无初速滑下,从P点滑上水平导轨,当A滑过距离s1=R时,与B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连.最后A恰好返回出发点P并停止.在A、B压缩弹簧过程始终未超过弹簧的弹性限度.已知滑块A和B质量相同(A、B可视为质点),且与导轨的滑动摩擦因数都为μ=0.1,重力加速度为g.试求:
如图所示,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平导轨上,弹簧处在原长状态.滑块A从半径为R的光滑$\frac{1}{4}$圆弧槽无初速滑下,从P点滑上水平导轨,当A滑过距离s1=R时,与B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连.最后A恰好返回出发点P并停止.在A、B压缩弹簧过程始终未超过弹簧的弹性限度.已知滑块A和B质量相同(A、B可视为质点),且与导轨的滑动摩擦因数都为μ=0.1,重力加速度为g.试求: