题目内容
20．
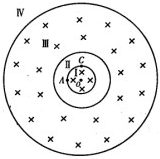如图所示，三个半径分别为R，2R，6R的同心圆将空间分为Ⅰ，Ⅱ，Ⅲ，Ⅳ四个区域，其中圆形区域Ⅰ和环形区域Ⅲ内有垂直纸面向里的匀强磁场，磁感应强度分别为B和$\frac{B}{2}$，一个质子从区域Ⅰ边界上的A点以速度v沿半径方向射入磁场，经磁场偏转恰好从区域Ⅰ边界上的C点飞出，AO垂直CO，则关于质子的运动，下列说法正确的是（ ）| A． | 质子最终将离开区域Ⅲ在区域Ⅳ匀速运动 | |
| B． | 质子最终将一直在区域Ⅲ内做匀速圆周运动 | |
| C． | 质子能够回到初始点A，且周而复始的运动 | |
| D． | 质子能够回到初始点A，且回到初始点前，在区域Ⅲ中运动的时间是在区域Ⅰ中运动时间的6倍 |
分析 （1）粒子垂直磁场方向进入磁场后在洛伦兹力的作用下做匀速圆周运动，要使粒子回到中心无磁场的圆形区域且过A点，画出运动轨迹，根据几何关系求解；
（2）粒子在区域Ⅰ中完成$\frac{1}{4}$个圆周运动，在区域Ⅲ中完成$\frac{3}{4}$个圆周运动，根据粒子偏转的角度与周期的关系，确定粒子运动的时间
解答 解：粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力：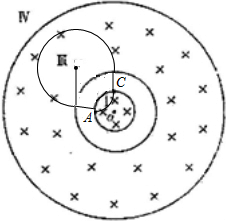
qvB=m$\frac{{v}^{2}}{r}$
粒子在区域Ⅰ中的半径：r1=$\frac{mv}{qB}$，
粒子在区域Ⅲ中的半径：r2=$\frac{mv}{q×\frac{B}{2}}$=$\frac{2mv}{qB}$=2r1，
画出粒子运动的轨迹如图，由图可得：质点能够回到初始点A，且周而复始的运动．故AB错误，C正确；
粒子在区域Ⅰ中完成$\frac{1}{4}$个圆周运动，粒子在区域Ⅰ中的周期：
T1=$\frac{2π{r}_{1}}{v}$=$\frac{2πm}{qB}$，粒子在区域Ⅰ中的时间：t1=$\frac{1}{4}$T1=$\frac{πm}{2qB}$，
在区域Ⅲ中完成$\frac{3}{4}$个圆周运动，粒子在区域Ⅲ中的周期：T2=$\frac{2π{r}_{2}}{v}$=$\frac{4πm}{qB}$，
粒子在区域Ⅲ中的时间：t2=$\frac{3}{4}$T2=$\frac{3πm}{qB}$=6t1．故D正确．
故选：CD．
点评 本题关键明确带电粒子的运动规律，求出粒子的半径，画出运动轨迹，然后根据几何关系求解即可．
练习册系列答案
阅读快车系列答案
相关题目
8．
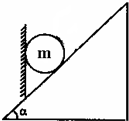如图所示，光滑球的质量为m，放在竖直挡板和倾角为α的固定斜面间．若缓慢转动挡板至与斜面垂直，此过程中（ ）
如图所示，光滑球的质量为m，放在竖直挡板和倾角为α的固定斜面间．若缓慢转动挡板至与斜面垂直，此过程中（ ）| A． | m对挡板的压力先减小后增大 | B． | m对挡板的压力逐渐减小 | ||
| C． | m对斜面的压力先减小后增大 | D． | m对斜面的压力逐渐增大 |
如图所示，小车质量为M=2kg，木块质量为m=0.5kg，静止在光滑水平地面上，t=0时刻给小车施加一个大小为F=20N的水平外力，拉动小车向右运动．木块和小车之间的动摩擦因数为μ=0.4，小车长度为10m，（g=10m/s2）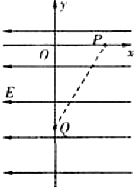
在地面上方某处的真空室里存在着水平方向的匀强电场，以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系．一质量为m、带电荷量为+q的微粒从点P（$\frac{\sqrt{3}}{3}$l，0）由静止释放后沿直线PQ运动．当微粒到达点Q（0，-l）的瞬间，撤去电场，同时加上一个垂直于纸面向外的匀强磁场（图中未画出），磁感应强度的大小B=$\frac{m}{q}$$\sqrt{\frac{3g}{2l}}$，该磁场有理想的下边界，其他方向范围无限大．已知重力加速度为g．求：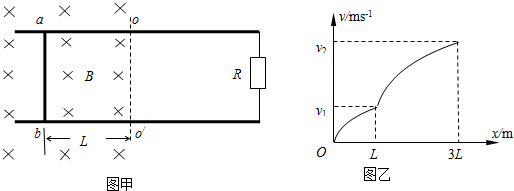
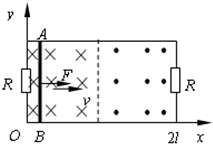矩形裸导线框长边的长度为2l，短边的长度为l，在两个短边上均接有阻值为R的电阻，其余部分电阻均不计．导线框的位置如图所示，线框内的磁场方向及分布情况如图，大小为$B={B_0}cos（{\frac{πx}{2l}}）$．一电阻为R的光滑导体棒AB与短边平行且与长边始终接触良好．起初导体棒处于x=0处，从t=0时刻起，导体棒AB在沿x方向的外力F的作用下做速度为v的匀速运动．试求：