题目内容
 质量为m=2kg的物体,放在水平面上,它与水平面之间的动摩擦因数μ=0.5,现对物体施F=30N的作用力,方向与水平成θ=37°(sin37°=0.6,cos37°=0.8)角斜向上,如图所示,(g=10m/s2)求:
质量为m=2kg的物体,放在水平面上,它与水平面之间的动摩擦因数μ=0.5,现对物体施F=30N的作用力,方向与水平成θ=37°(sin37°=0.6,cos37°=0.8)角斜向上,如图所示,(g=10m/s2)求:
(1)物体运动的加速度多大?
(2)物体在力F作用下经4s通过的位移是多大?
(3)如果力F作用经4s而撤去,则撤去F后物体运动的加速度多大?
解:(1)物体受力如图:
水平方向有:Fcosθ-f=ma
竖直方向有:N+Fsinθ=G
即N=G-Fsinθ
f=μN
故:Fcos37°-μ(mg-Fsin37°)=ma
解得:a=6m/s2
(2)由位移表达式可得x= at2=48m
at2=48m
(3)撤去F后,物体只受摩擦力,其加速度为:
a'=-μg=-5m/s2
答:(1)物体运动的加速度为6m/s2
(2)物体在力F作用下经4s通过的位移是48m
(3)如果力F作用经4s而撤去,则撤去F后物体运动的加速度的大小为5m/s2
分析:根据牛顿第二定律求出加速度的大小,再根据时间位移公式求出4s末的位移,通过牛顿第二定律求出撤去拉力后的加速度.
点评:本题是比较简单的运动和受力分析,此类题目通常在受力是要列运动方向的牛顿第二定律和垂直于运动方向的平衡方程.

水平方向有:Fcosθ-f=ma
竖直方向有:N+Fsinθ=G
即N=G-Fsinθ
f=μN
故:Fcos37°-μ(mg-Fsin37°)=ma
解得:a=6m/s2
(2)由位移表达式可得x=
 at2=48m
at2=48m(3)撤去F后,物体只受摩擦力,其加速度为:
a'=-μg=-5m/s2
答:(1)物体运动的加速度为6m/s2
(2)物体在力F作用下经4s通过的位移是48m
(3)如果力F作用经4s而撤去,则撤去F后物体运动的加速度的大小为5m/s2
分析:根据牛顿第二定律求出加速度的大小,再根据时间位移公式求出4s末的位移,通过牛顿第二定律求出撤去拉力后的加速度.
点评:本题是比较简单的运动和受力分析,此类题目通常在受力是要列运动方向的牛顿第二定律和垂直于运动方向的平衡方程.

练习册系列答案
相关题目
 质量为m=2kg的物块由倾角为θ=30°,从斜面顶端匀速下滑,则物块与斜面间的动摩擦因数?=
质量为m=2kg的物块由倾角为θ=30°,从斜面顶端匀速下滑,则物块与斜面间的动摩擦因数?= 如图所示,一辆质量为M=6kg的小车静止在光滑的水平面上,另一质量为m=2kg的物块(可视为质点)静止在小车上的A点;在物块和小车右侧的挡板之间夹有一被压缩的轻质弹簧(弹簧和物块不相连),弹簧的弹性势能为4J,物块和挡板之间用细线连结.已知物块和小车之间的动摩擦因数μ=0.2.某时刻将细线烧断,弹簧将物块弹开,最后物块停在小车上的B点,取g=10m/s2.
如图所示,一辆质量为M=6kg的小车静止在光滑的水平面上,另一质量为m=2kg的物块(可视为质点)静止在小车上的A点;在物块和小车右侧的挡板之间夹有一被压缩的轻质弹簧(弹簧和物块不相连),弹簧的弹性势能为4J,物块和挡板之间用细线连结.已知物块和小车之间的动摩擦因数μ=0.2.某时刻将细线烧断,弹簧将物块弹开,最后物块停在小车上的B点,取g=10m/s2.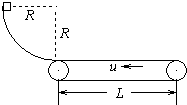 如图所示,一个质量为M=2kg的物块(可视为质点)从光滑四分之一圆弧轨道顶端由静止滑下,圆弧轨道半径R=0.8m,到达底端时恰好进入与圆弧轨道底端相切的水平传送带,传送带由一电动机驱动着匀速向左转动,速度大小为V=3m/s,已知物块与传送带间的动摩擦因数为μ=0.1,两皮带轮之间的距离为L=6m,重力加速度g=10m/s2.求:
如图所示,一个质量为M=2kg的物块(可视为质点)从光滑四分之一圆弧轨道顶端由静止滑下,圆弧轨道半径R=0.8m,到达底端时恰好进入与圆弧轨道底端相切的水平传送带,传送带由一电动机驱动着匀速向左转动,速度大小为V=3m/s,已知物块与传送带间的动摩擦因数为μ=0.1,两皮带轮之间的距离为L=6m,重力加速度g=10m/s2.求: 如图所示,在光滑水平面上静止着一块质量为M=5kg的长方体木板A,木板的左端静止放置着一质量为m=2kg的物块B,已知AB之间动摩擦因数μ=0.5,经过实验发现当对物块B施加一个大小为16N水平向右的拉力F后经过2s物块B被拉到木板的右端,g取10m/s2,求:
如图所示,在光滑水平面上静止着一块质量为M=5kg的长方体木板A,木板的左端静止放置着一质量为m=2kg的物块B,已知AB之间动摩擦因数μ=0.5,经过实验发现当对物块B施加一个大小为16N水平向右的拉力F后经过2s物块B被拉到木板的右端,g取10m/s2,求: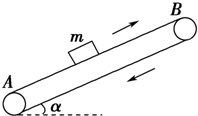 如图所示,传送带两轮A、B的距离L=11m,皮带以恒定速度v=2m/s运动,现将一质量为m=2kg的物块无初速度地放在A端,若物体与传送带间的动摩擦因数为μ=0.8,传送带的倾角为α=37°,那么(g取10m/s2,cos37°=0.8)
如图所示,传送带两轮A、B的距离L=11m,皮带以恒定速度v=2m/s运动,现将一质量为m=2kg的物块无初速度地放在A端,若物体与传送带间的动摩擦因数为μ=0.8,传送带的倾角为α=37°,那么(g取10m/s2,cos37°=0.8)