题目内容
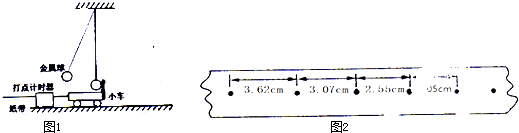
某同学设计了如图1所示的装置,利用米尺、秒表、轻绳、轻滑轮、轨道、滑块、托盘和砝码等器材来测定滑块和轨道间的动摩擦因数μ.滑块和托盘上分别放有若干砝码,滑块质量为M,滑块上砝码总质量为m′,托盘和盘中砝码的总质量为m.实验中,滑块在水平轨道上从A到B做初速为零的匀加速直线运动,重力加速度g取10m/s2.
①为测量滑块的加速度a,须测出它在A、B间运动的
②根据牛顿运动定律得到a与m的关系为:a=
m-μg他想通过多次改变m,测出相应的a值,并利用上式来计算μ.若要求a是m的一次函数,必须使上式中的
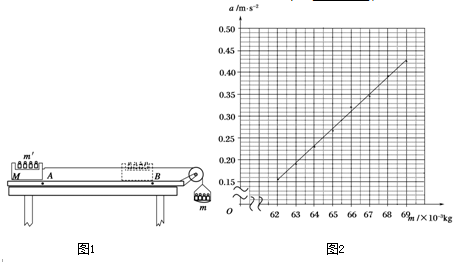
③实验得到a与m的关系如图2所示,由此可知μ=

①为测量滑块的加速度a,须测出它在A、B间运动的
位移s
位移s
与时间t
时间t
,计算a的运动学公式是a=
| 2s |
| t2 |
a=
;| 2s |
| t2 |
②根据牛顿运动定律得到a与m的关系为:a=
| (1+μ)g |
| M+(m′+m) |
m′+m
m′+m
保持不变,实验中应将从托盘中取出的砝码置于滑块上
滑块上
;③实验得到a与m的关系如图2所示,由此可知μ=
0.23
0.23
(取两位有效数字).分析:①在初速度为零的匀加速直线运动中共有s、t、a、v四个常用量.欲测加速度a则必须测出s、t、v中的任意两个,但是速度v不容易直接测量,故须测出位移s和时间t,再根据a=
求a.
②把a=
m-μg与一次函数y=kx+b相对应,当与k相对应的
为定值时,即m′+m保持不变时,a是m的一次函数.实验时只需将砝码从托盘中取出并置于滑块上即可达到目的.由图象斜率去算出摩擦因数
| 2s |
| t2 |
②把a=
| (1+μ)g |
| M+(m′+m) |
| (1+μ)g |
| M+(m′+m) |
解答:解:①滑块在水平轨道上从A到B做初速为零的匀加速直线运动,根据s=
at2,得a=
,
所以需要测量的是位移s和时间t.
②对整体进行研究,根据牛顿第二定律得:a=
=
m-μg.
若要求a是m的一次函数必须使
为定值,即m′+m保持不变时,在增大m时等量减小m′,
所以实验中应将从托盘中取出的砝码置于滑块上.
③将
取为k,有:k=
=
,在图象上取两点将坐标代入
解得:μ=0.23(在0.21到0.25之间是正确的)
故答案为:①位移s,时间t,a=
;②m′+m,滑块上; ③0.23(0.21~0.25).
| 1 |
| 2 |
| 2s |
| t2 |
所以需要测量的是位移s和时间t.
②对整体进行研究,根据牛顿第二定律得:a=
| mg-μ(M+m′)g |
| M+m+m′ |
| (1+μ)g |
| M+(m′+m) |
若要求a是m的一次函数必须使
| (1+μ)g |
| M+(m′+m) |
所以实验中应将从托盘中取出的砝码置于滑块上.
③将
| (1+μ)g |
| M+(m′+m) |
| a1+μg |
| m1 |
| a2+μg |
| m2 |
解得:μ=0.23(在0.21到0.25之间是正确的)
故答案为:①位移s,时间t,a=
| 2s |
| t2 |
点评:通过作出两个量的图象,然后由图象去寻求未知量与已知量的关系.
运用数学知识和物理量之间关系式结合起来求解.
运用数学知识和物理量之间关系式结合起来求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

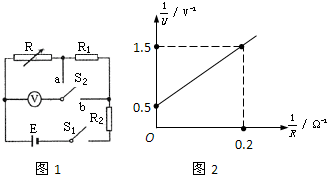 (2010?烟台一模)某同学设计了如图1所示的电路测电源电动势E及电阻R1和R2的阻值.实验器材有:待测电源E(不计内阻),待测电阻R1,待测电阻R2,电压表V(量程为3.0V,内阻很大),电阻箱R(0-99.99Ω),单刀单掷开关S1,单刀双掷开关S2,导线若干.
(2010?烟台一模)某同学设计了如图1所示的电路测电源电动势E及电阻R1和R2的阻值.实验器材有:待测电源E(不计内阻),待测电阻R1,待测电阻R2,电压表V(量程为3.0V,内阻很大),电阻箱R(0-99.99Ω),单刀单掷开关S1,单刀双掷开关S2,导线若干.