题目内容
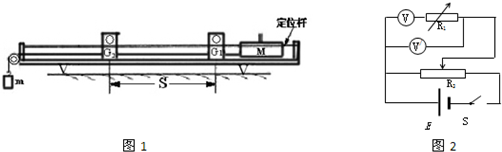
为了探究加速度与力的关系,某同学设计了如图1所示的实验装置,带滑轮的长木板水平放置,板上有两个光电门相距为d,滑块通过细线与重物相连,细线的拉力F大小等于力传感器的示数.让滑块从光电门1由静止释放,记下滑到光电门2的时间t,改变重物质量来改变细绳拉力大小,重复以上操作5次,得到下列表格中5组数据.
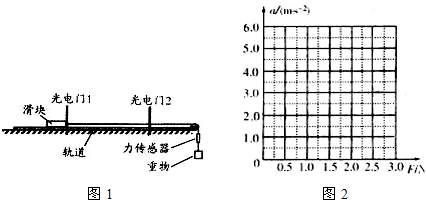
(1)若测得两光电门之间距离为d=0.5m,运动时间t=0.5s,则a=
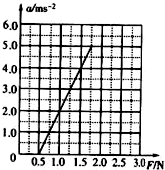
(2)依据表中数据在如图2中画出a-F图象.
(3)由图象可得滑块质量m=

| 次数 | a/(m?s-2) | F/N |
| 1 | 1.0 | 0.76 |
| 2 | 2.0 | 0.99 |
| 3 | 3.0 | 1.23 |
| 4 | 4.0 | 1.50 |
| 5 | 5.0 | 1.76 |
4.0
4.0
m/s2;(2)依据表中数据在如图2中画出a-F图象.
(3)由图象可得滑块质量m=
0.25
0.25
kg,滑块和轨道间的动摩擦因数μ=0.2
0.2
.g=10m/s2.分析:(1)根据运动学公式x=
at2求解加速度.
(2)依据表中数据运用描点法作出图象
(3)知道滑块运动的加速度a和所受拉力F的关系图象斜率等于滑块质量的倒数.对滑块受力分析,根据牛顿第二定律求解.
| 1 |
| 2 |
(2)依据表中数据运用描点法作出图象
(3)知道滑块运动的加速度a和所受拉力F的关系图象斜率等于滑块质量的倒数.对滑块受力分析,根据牛顿第二定律求解.
解答:解:(1)根据运动学公式x=
at2得
a=
=
=4.0m/s2;
(2)依据表中数据运用描点法作出图象:
(3)根据F-μmg=ma得a=
-μg,所以滑块运动的加速度a和所受拉力F的关系图象斜率等于滑块质量的倒数.
由图形得加速度a和所受拉力F的关系图象斜率k=4,所以滑块质量m=0.25Kg,
由图形得,当F=0.5N时,滑块就要开始滑动,所以滑块与轨道间的最大静摩擦力等于0.5N,
而最大静摩擦力等于滑动摩擦力,即μmg=0.5N,
解得μ=0.2
故答案为:(1)4.0;(2)如图;(3)0.25,0.2
| 1 |
| 2 |
a=
| 2x |
| t2 |
| 2×0.5 |
| (0.5)2 |
(2)依据表中数据运用描点法作出图象:

(3)根据F-μmg=ma得a=
| F |
| m |
由图形得加速度a和所受拉力F的关系图象斜率k=4,所以滑块质量m=0.25Kg,
由图形得,当F=0.5N时,滑块就要开始滑动,所以滑块与轨道间的最大静摩擦力等于0.5N,
而最大静摩擦力等于滑动摩擦力,即μmg=0.5N,
解得μ=0.2
故答案为:(1)4.0;(2)如图;(3)0.25,0.2
点评:解决该题关键要掌握牛顿第二定律和运动学公式的应用,运用数学知识和物理量之间关系式结合起来求解.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目