题目内容
20.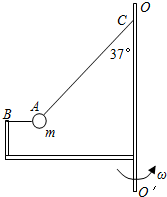 如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m=1kg,细线AC长l=1m.(重力加速度g取10m/s2,sin37°=$\frac{3}{5},cos37°=\frac{4}{5}$)
如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m=1kg,细线AC长l=1m.(重力加速度g取10m/s2,sin37°=$\frac{3}{5},cos37°=\frac{4}{5}$)(1)若装置匀速转动的角速度为ω1时,细线AB上的张力为0而AC与竖直方向的夹角仍为37°,求角速度ω1的大小;
(2)若装置匀速转动的角速度为ω2=$\sqrt{10}$rad/s,求细线AB的拉力.
分析 (1)当细线AB张力为零时,绳子AC拉力和重力的合力提供向心力,根据牛顿第二定律求出角速度的大小.
(2)装置匀速转动的角速度ω2=$\sqrt{10}$rad/s,小于第一问中的角速度,根据牛顿第二定律求细线AB的拉力.
解答 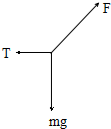 解:(1)当细线AB上的张力为0时,小球的重力和细线AC张力的合力提供小球圆周运动的向心力,有:
解:(1)当细线AB上的张力为0时,小球的重力和细线AC张力的合力提供小球圆周运动的向心力,有:
mgtan37°=mω12lsin37°
解得:ω1=$\sqrt{\frac{g}{lcos37°}}$=$\sqrt{\frac{10}{1×0.8}}$=$\frac{5\sqrt{2}}{2}$rad/s.
(2)由于ω2<ω1,则细线AB上有拉力,为T,AC线上的拉力为F.根据牛顿第二定律得:
Fcos37°=mg
Fsin37°-T=mω22lsin37°
解得:F=12.5N,T=1.5N
答:(1)角速度ω1的大小为$\frac{5\sqrt{2}}{2}$rad/s;
(2)若装置匀速转动的角速度为ω2=$\sqrt{10}$rad/s,细线AB的拉力是1.5N.
点评 解决本题的关键理清小球做圆周运动的向心力来源,确定小球运动过程中的临界状态,运用牛顿第二定律进行求解.

练习册系列答案
相关题目
8. 如图所示,质量为m的滑块与轨道间的动摩擦因数为μ,当滑块从A滑到B的过程中,受到的摩擦力的最大值为F,则( )
如图所示,质量为m的滑块与轨道间的动摩擦因数为μ,当滑块从A滑到B的过程中,受到的摩擦力的最大值为F,则( )
 如图所示,质量为m的滑块与轨道间的动摩擦因数为μ,当滑块从A滑到B的过程中,受到的摩擦力的最大值为F,则( )
如图所示,质量为m的滑块与轨道间的动摩擦因数为μ,当滑块从A滑到B的过程中,受到的摩擦力的最大值为F,则( )| A. | F=μmg | B. | F>μmg | ||
| C. | F<μmg | D. | 无法确定F与μmg的大小关系 |
15.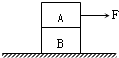 如图所示,A、B两物体叠放在水平面上,水平力F作用在A上,使两者一起向右做匀速直线运动,下列判断中正确的是( )
如图所示,A、B两物体叠放在水平面上,水平力F作用在A上,使两者一起向右做匀速直线运动,下列判断中正确的是( )
 如图所示,A、B两物体叠放在水平面上,水平力F作用在A上,使两者一起向右做匀速直线运动,下列判断中正确的是( )
如图所示,A、B两物体叠放在水平面上,水平力F作用在A上,使两者一起向右做匀速直线运动,下列判断中正确的是( )| A. | A对B的摩擦力大小为F,方向向左 | |
| B. | A、B两物体间有两对作用力与反作用力 | |
| C. | A物体受两对平衡力 | |
| D. | B对A的作用力与F的合力方向竖直向下 |
5.下列说法中指时刻的有( )
| A. | 新闻30分每天中午12点开播 | B. | 一场足球比赛90分钟 | ||
| C. | 火车到站运行9时20分 | D. | 数学测试的时间是45min |
12. 甲、乙两个物体在同一直线上运动,它们的速度-时间图象如图所示,由图象可知( )
甲、乙两个物体在同一直线上运动,它们的速度-时间图象如图所示,由图象可知( )
 甲、乙两个物体在同一直线上运动,它们的速度-时间图象如图所示,由图象可知( )
甲、乙两个物体在同一直线上运动,它们的速度-时间图象如图所示,由图象可知( )| A. | 在t1时刻,甲、乙的位移相同 | |
| B. | 在t1时刻,甲和乙的速度相同 | |
| C. | 在t2时刻,甲和乙的速度方向相同,加速度方向相反 | |
| D. | 在t2时刻,甲和乙的速度方向相同,加速度方向也相同 |
10. 如图所示为A、B两质点作直线运动的速度-时间图象,A、B两斜线互相平行,由此可以看出( )
如图所示为A、B两质点作直线运动的速度-时间图象,A、B两斜线互相平行,由此可以看出( )
 如图所示为A、B两质点作直线运动的速度-时间图象,A、B两斜线互相平行,由此可以看出( )
如图所示为A、B两质点作直线运动的速度-时间图象,A、B两斜线互相平行,由此可以看出( )| A. | 两质点具有相同的加速度,而有不同的初速度 | |
| B. | 两质点经过相同的运动时间,各自速度的增加量也相同 | |
| C. | 它们是同时出发的,出发后两质点之间的距离越来越大 | |
| D. | 由于不知道出发点的位置关系,不可能确定出发后两质点之间的距离是如何变化的 |
 如图所示,是一游客在北方哈尔滨某滑雪场滑雪时从高台上滑下的情况,滑到滑道端点A处时沿水平方向滑出,落到倾角为30°的斜坡上B点.已知A点到斜坡的竖直距离为4m,AB=78m,不计空气阻力,取g=10m/s2,求游客离开A处时的速度V0.
如图所示,是一游客在北方哈尔滨某滑雪场滑雪时从高台上滑下的情况,滑到滑道端点A处时沿水平方向滑出,落到倾角为30°的斜坡上B点.已知A点到斜坡的竖直距离为4m,AB=78m,不计空气阻力,取g=10m/s2,求游客离开A处时的速度V0. 如图所示,一斜面体M=3kg 与粗糙的水平地面摩擦因数μ=0.25,在水平推力F作用下,与位于光滑的斜面上的物体m=0.5kg保持相对静止一起向左做匀加速运动.
如图所示,一斜面体M=3kg 与粗糙的水平地面摩擦因数μ=0.25,在水平推力F作用下,与位于光滑的斜面上的物体m=0.5kg保持相对静止一起向左做匀加速运动.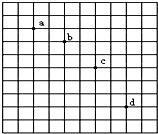 在研究平抛运动的实验中,小球必须每次从斜槽上的同一位置落下,是为了使小球离开斜槽末端的速度不变,同时需要调节斜槽末端水平.在坐标纸的平抛运动轨迹上任取一点,用刻度尺量出它的坐标x和y,则实验中的小球的初速度表达式为v0=$x\sqrt{\frac{g}{2y}}$.如图是某同学做平抛运动实验时,用一张印有小方格的纸记录轨迹,小方格的边长L=2.5cm,若小球在平抛运动途中的几个位
在研究平抛运动的实验中,小球必须每次从斜槽上的同一位置落下,是为了使小球离开斜槽末端的速度不变,同时需要调节斜槽末端水平.在坐标纸的平抛运动轨迹上任取一点,用刻度尺量出它的坐标x和y,则实验中的小球的初速度表达式为v0=$x\sqrt{\frac{g}{2y}}$.如图是某同学做平抛运动实验时,用一张印有小方格的纸记录轨迹,小方格的边长L=2.5cm,若小球在平抛运动途中的几个位