题目内容
11. 如图所示,一斜面体M=3kg 与粗糙的水平地面摩擦因数μ=0.25,在水平推力F作用下,与位于光滑的斜面上的物体m=0.5kg保持相对静止一起向左做匀加速运动.
如图所示,一斜面体M=3kg 与粗糙的水平地面摩擦因数μ=0.25,在水平推力F作用下,与位于光滑的斜面上的物体m=0.5kg保持相对静止一起向左做匀加速运动.(已知斜面体倾角θ=37°,sinθ=0.6,cosθ=0.8,g=10m/s2)求:
(1)M与m的共同加速度大小
(2)水平推力的大小.
分析 (1)物体m向左做匀加速运动,合力水平向左,对m进行受力分析,根据牛顿第二定律求解加速度.
(2)再对AB整体运用牛顿第二定律即可求解F.
解答 解:(1)以物体m为研究对象,根据牛顿第二定律得
mgtan37°=ma,所以a=7.5m/s2
(2)对整体,根据牛顿第二定律得:
F-μ(M+m)g=(M+m)a
可得 F=(M+m)(μg+a)=(3+0.5)×(0.25×10+7.5)N=35N
答:
(1)M与m的共同加速度大小是7.5m/s2.
(2)水平推力的大小是35N.
点评 本题的关键要灵活选取研究对象,抓住物体与斜面加速度相同的特点,可采用隔离法,也可以运用整体法研究.

练习册系列答案
相关题目
2.甲、乙两物体都在做匀速圆周运动,以下关于它们的向心加速度大小判断正确的是( )
| A. | 它们的线速度相等,乙的半径小,则甲的向心加速度较大 | |
| B. | 它们的周期相等,甲的半径大,则甲的向心加速度较大 | |
| C. | 它们的角速度相等,乙的线速度小,则乙的向心加速度较大 | |
| D. | 它们的线速度相等,在相同时间内甲与圆心的连线扫过的角度比乙的大,则乙的向心加速度较大 |
19.下面的几个速度中表示平均速度的是( )
| A. | 子弹射出枪口的速度是800 m/s,以 790 m/s的速度击中目标 | |
| B. | 汽车从甲站行驶到乙站的速度是40 km/h | |
| C. | 运动员百米冲刺时通过终点的速度是10.8m/s | |
| D. | 小球第3 s末的速度是6 m/s |
6.如图所示,用绳竖直悬挂的小球下端与一静止的斜面接触,则以下说法正确的是( )


| A. | 小球只受两个力作用 | |
| B. | 小球可能受三个力作用 | |
| C. | 小球可能受四个力作用 | |
| D. | 绳对球的拉力和球对绳拉力等大反向,作用效果抵消,故小球受力平衡 |
16.甲、乙两列军队急行军,从同一地点出发沿不同路径到达相同的目的地,则( )
| A. | 甲、乙的路程必定相同 | B. | 甲、乙的位移必定相同 | ||
| C. | 甲、乙的位移可能不同 | D. | 甲、乙的行军所花的时间一定相同 |
1.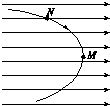 如图,一带负电粒子以某速度进入水平向右的匀强电场中,在电场力作用下形成图中所示的运动轨迹,M和N是轨迹上的两点,其中M点在轨迹的最右点.不计重力,下列表述正确的是( )
如图,一带负电粒子以某速度进入水平向右的匀强电场中,在电场力作用下形成图中所示的运动轨迹,M和N是轨迹上的两点,其中M点在轨迹的最右点.不计重力,下列表述正确的是( )
 如图,一带负电粒子以某速度进入水平向右的匀强电场中,在电场力作用下形成图中所示的运动轨迹,M和N是轨迹上的两点,其中M点在轨迹的最右点.不计重力,下列表述正确的是( )
如图,一带负电粒子以某速度进入水平向右的匀强电场中,在电场力作用下形成图中所示的运动轨迹,M和N是轨迹上的两点,其中M点在轨迹的最右点.不计重力,下列表述正确的是( )| A. | 粒子在M点的速率最大 | B. | 粒子所受电场力与电场方向相反 | ||
| C. | 粒子在电场中的加速度不变 | D. | 粒子在电场中的电势能始终在增加 |
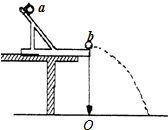 某同学用如图所示装置来验证动量守恒定律,相应的操作步骤如下:
某同学用如图所示装置来验证动量守恒定律,相应的操作步骤如下:
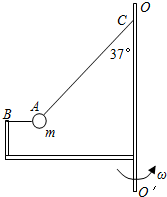 如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m=1kg,细线AC长l=1m.(重力加速度g取10m/s2,sin37°=$\frac{3}{5},cos37°=\frac{4}{5}$)
如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m=1kg,细线AC长l=1m.(重力加速度g取10m/s2,sin37°=$\frac{3}{5},cos37°=\frac{4}{5}$)