Question

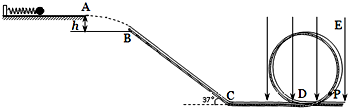
如图所示，足够长的光滑绝缘水平台左端固定一被压缩的绝缘轻质弹簧，一个质量m=0.04kg、电量q=+2×10^-4c的可视为质点的带电小球与弹簧接触但不栓接．某一瞬间释放弹簧弹出小球，小球从水平台右端A点飞出，恰好能没有碰撞地落到粗糙倾斜轨道的最高B点，并沿轨道滑下．已知AB的竖直高度h=0.45m，倾斜轨道与水平方向夹角为α=37°、倾斜轨道长为L=2.0m，带电小球与倾斜轨道的动摩擦因数μ=0.5．倾斜轨道通过光滑水平轨道CD与光滑竖直圆轨道相连，在C点没有能量损失，所有轨道都绝缘，运动过程小球的电量保持不变．只有过山车模型的竖直圆轨道处在范围足够大竖直向下的匀强电场中，场强E=2.0×10³V/m．（cos37°=0.8，sin37°=0.6，取g=10m/s²）求：
（1）被释放前弹簧的弹性势能？
（2）要使小球不离开轨道（水平轨道足够长），竖直圆弧轨道的半径应该满足什么条件？
（3）如果竖直圆弧轨道的半径R=0.9m，小球进入轨道后可以有多少次通过竖直圆轨道上距水平轨道高为0.01m的某一点P？

Answer 1

分析：（1）释放弹簧后弹簧的弹性势能转化为小球的动能．先根据小球从A到B平抛运动过程，求出小球到B点时竖直分速度，由速度的分解求出到A点的速度，即可根据机械能守恒求解被释放前弹簧的弹性势能．
（2）要使小球不离开轨道，有两种情况：第一种情况：是恰好过竖直圆轨道最高点时，先由牛顿第二定律和向心力知识求出到最高点的速度，再由动能定理求解轨道半径．第二种情况：小球恰好到竖直圆轨道最右端，由动能定理求解轨道半径．
（3）根据R=0.9m与上题结果中轨道半径R₂的关系，知道小球冲上圆轨道H₁=0.825m高度时速度变为0，然后返回倾斜轨道h₁高处再滑下，然后再次进入圆轨道达到的高度为H₂．对两个过程，由动能定理求出H₂与H₁的关系，归纳得到n次上升高度H_n，运用数学知识求解．

解答：解：（1）A到B平抛运动：v_y²=2gh
代入数据解得：v_y=

2gh

=

2×10×0.45

m/s=3m/s
B点：tan37°=

vy

vx

得：v_x=v_A=

vy

tan37°

=

3

3 4

m/s=4m/s
被释放前弹簧的弹性势能：E_p=

1

2

m

v

2 A

=

1

2

×0.04×42J=0.32J；
（2）B点：v_B=

v 2 x + v 2 y

=

42+32

m/s=5m/s
B到C：（mgsin37°-μmgcos37°）L=

1

2

m

v

2 C

-

1

2

m

v

2 B

，
代入数据解得：v_C=

33

m/s
①恰好过竖直圆轨道最高点时：mg+qE=m

v 2 0

R1

，
  qE=0.4N=mg
从C到圆轨道最高点：-（mg+qE）2R₁=

1

2

m

v

2 0

-

1

2

m

v

2 C

得：R₁=0.33m
②恰好到竖直圆轨道最右端时：-（mg+qE）R₂=0-

1

2

m

v

2 C

得：R₂=0.825m
要使小球不离开轨道，竖直圆弧轨道的半径R≤0.33m或R≥0，825m；
（3）R=0.9m＞R₂，小球冲上圆轨道H₁=0.825m高度时速度变为0，然后返回倾斜轨道h₁高处再滑下，然后再次进入圆轨道达到的高度为H₂．
有：（mg+qE）H₁=mgh₁+μmgh₁?

4

3

，
    （mg+qE）H₂=mgh₁-μmgh₁?

4

3

，
同除得：H₂=

1- 4 3 μ

1+ 4 3 μ

H₁=

1

5

H₁之后物块在竖直圆轨道和倾斜轨道之间往返运动．
同理：n次上升高度H_n=（

1

5

）^n-1H₁（n＞0）为一等比数列．  
(

1

5

)n-1×0.825≤0.01，当n=4时，上升的最大高度小于0.01m
则小球共有6次通过距水平轨道高为0.01m的某一点．  
答：
（1）被释放前弹簧的弹性势能为0.32J．
（2）要使小球不离开轨道（水平轨道足够长），竖直圆弧轨道的半径R≤0.33m或R≥0，825m．
（3）如果竖直圆弧轨道的半径R=0.9m，小球进入轨道后可以有6次通过竖直圆轨道上距水平轨道高为0.01m的某一点P．

点评：本题是复杂的力电综合题，明确研究对象的运动过程是解决问题的前提，根据题目已知条件和求解的物理量选择物理规律解决问题．要注意小球运动过程中各个物理量的变化．