题目内容
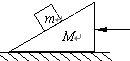如图，质量m=1kg的物块放在倾角为θ的斜面上，斜面体质量M=2kg，斜面与物块间的动摩擦因数μ=0.2，地面光滑，θ=37°，现对斜面体施一水平推力F，要使物体m相对斜面静止，力F应为多大？（ g=10m/s2，设物体与斜面的最大静摩擦力等于滑动摩擦力）分析：用极限法把F推向两个极端来分析：当F较小（趋近于0）时，由于μ＜tanθ，因此物块将沿斜面加速下滑；若F较大（足够大）时，物块将相对斜面向上滑，因此F不能太小，也不能太大，根据牛顿第二定律，运用整体隔离法求出F的取值范围．
解答：解：（1）设物块处于相对斜面向下滑的临界状态时推力为F1，此时物块受力如图，取加速度a方向为x轴正向，对m：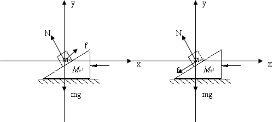
x方向：Nsinθ-μNcosθ=ma1?
y方向：Ncosθ+μNsinθ-mg=0
对整体：F1=（M+m）a1?
把已知代入并解得：a1=4.78m/s2?F1=14.34N
（2）设物块处于相对斜面向上滑的临界状态时推力为F2，此时物块受力如图，对m：
x方向：Nsinθ+μNcosθ=ma2?y方向：Ncosθ-μNsinθ-mg=0
对整体：F2=（M+m）a2
把已知代入并解得a2=11.2 m/s2，F2=33.6N
∴14.34N≤F≤33.6N
答：F的取值范围为14.34N≤F≤33.6N．
x方向：Nsinθ-μNcosθ=ma1?
y方向：Ncosθ+μNsinθ-mg=0
对整体：F1=（M+m）a1?
把已知代入并解得：a1=4.78m/s2?F1=14.34N
（2）设物块处于相对斜面向上滑的临界状态时推力为F2，此时物块受力如图，对m：
x方向：Nsinθ+μNcosθ=ma2?y方向：Ncosθ-μNsinθ-mg=0
对整体：F2=（M+m）a2
把已知代入并解得a2=11.2 m/s2，F2=33.6N
∴14.34N≤F≤33.6N
答：F的取值范围为14.34N≤F≤33.6N．
点评：解决本题的关键能够正确地受力分析，抓住临界状态，运用牛顿第二定律进行求解，注意整体法和隔离法的运用．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
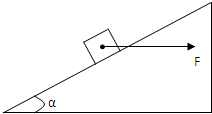如图，质量m=1kg的物体在F=20N水平向右的拉力作用下由静止开始沿足够长的斜面向上滑动，斜面固定不动且与水平方向成α=37°角，物体与斜面之间的动摩擦因数μ=0.25，拉力F作用物体2s后撤去．
