题目内容
(2012?惠州二模)如图,质量M=1kg的木板静止在水平面上,质量m=1kg、大小可以忽略的铁块静止在木板的右端.设最大摩擦力等于滑动摩擦力,已知木板与地面间的动摩擦因数μ1=0.1,铁块与木板之间的动摩擦因数μ2=0.4,取g=10m/s2.现给铁块施加一个水平向左的力F.
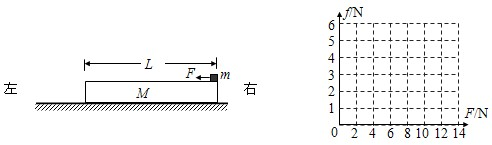
(1)若力F恒为8N,经1s铁块运动到木板的左端.求:木板的长度
(2)若力F从零开始逐渐增加,且木板足够长.试通过分析与计算,在图中作出铁块受到的摩擦力f随力F大小变化的图象.

(1)若力F恒为8N,经1s铁块运动到木板的左端.求:木板的长度
(2)若力F从零开始逐渐增加,且木板足够长.试通过分析与计算,在图中作出铁块受到的摩擦力f随力F大小变化的图象.
分析:(1)根据牛顿第二定律分别求出铁块和木板的加速度,铁块相对木板的位移等于木板的长度时铁块滑到木板的左端,由位移公式求解木板的长度.
(2)若力F从零开始逐渐增加,根据F与铁块的最大静摩擦力关系,以及铁块对木板的滑动摩擦力与木板所受地面的最大 静摩擦力,分析铁块的运动状态,确定平衡条件或牛顿第二定律研究铁块所受的摩擦力.
(2)若力F从零开始逐渐增加,根据F与铁块的最大静摩擦力关系,以及铁块对木板的滑动摩擦力与木板所受地面的最大 静摩擦力,分析铁块的运动状态,确定平衡条件或牛顿第二定律研究铁块所受的摩擦力.
解答: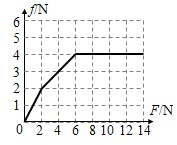 解:(1)由牛顿第二定律:
解:(1)由牛顿第二定律:
对铁块:F-μ2mg=ma1…①
对木板:μ2mg-μ1(M+m)g=Ma2…②
设木板的长度为L,经时间t铁块运动到木板的左端,则
s木=
a2t2…③
s铁=
a1t2…④
又:s铁-s木=L…⑤
联立①②③④⑤解得:L=1m…⑥
(2)(i)当F≤μ1(m+M)g=2N时,系统没有被拉动,静摩擦力与外力平衡,即有:f=F
(ii)当F>μ1(m+M)g=2N时,如果M、m相对静止,铁块与木板有相同的加速度a,则:
F-μ1(m+M)g=(m+M)a…⑦
F-f=ma…⑧
解得:F=2f-2…⑨
此时:f≤μ1mg=4N,也即F≤6N…⑩
所以:当2N<F≤6N时,f=
+1(N)
(iii)当F>6N时,M、m相对滑动,此时铁块受到的摩擦力为:
f=μ2mg=4N
f-F图象如图所示
答:
(1)木板的长度为1m.
(2)f-F图象如图所示.
 解:(1)由牛顿第二定律:
解:(1)由牛顿第二定律:对铁块:F-μ2mg=ma1…①
对木板:μ2mg-μ1(M+m)g=Ma2…②
设木板的长度为L,经时间t铁块运动到木板的左端,则
s木=
| 1 |
| 2 |
s铁=
| 1 |
| 2 |
又:s铁-s木=L…⑤
联立①②③④⑤解得:L=1m…⑥
(2)(i)当F≤μ1(m+M)g=2N时,系统没有被拉动,静摩擦力与外力平衡,即有:f=F
(ii)当F>μ1(m+M)g=2N时,如果M、m相对静止,铁块与木板有相同的加速度a,则:
F-μ1(m+M)g=(m+M)a…⑦
F-f=ma…⑧
解得:F=2f-2…⑨
此时:f≤μ1mg=4N,也即F≤6N…⑩
所以:当2N<F≤6N时,f=
| F |
| 2 |
(iii)当F>6N时,M、m相对滑动,此时铁块受到的摩擦力为:
f=μ2mg=4N
f-F图象如图所示
答:
(1)木板的长度为1m.
(2)f-F图象如图所示.
点评:第1题关键抓住两个物体的位移与木板长度的关系.第2题根据F与最大静摩擦力的关系,分析物体的运动状态是关键,要进行讨论.

练习册系列答案
相关题目