题目内容
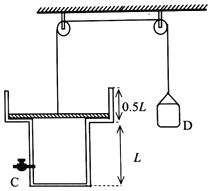
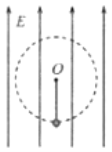
【题目】如图所示,空间存在竖直向上的匀强电场,长为L的绝缘细线的一端固定于O点,另一端系着一个质量为m、电荷量为![]() 的带电小球,小球恰好在竖直平面内做匀速圆周运动当小球运动到最低点时,只将电场反向,小球仍能在竖直平面内做完整的圆周运动不计空气阻力重力加速度为g,求:
的带电小球,小球恰好在竖直平面内做匀速圆周运动当小球运动到最低点时,只将电场反向,小球仍能在竖直平面内做完整的圆周运动不计空气阻力重力加速度为g,求:
(1)电场强度E的大小;
(2)小球运动到最低点时速度的最小值v.
【答案】(1)![]() (2)
(2)![]()
【解析】
解:(1)小球在电场中受到重力、电场力和细线的拉力作用,匀强电场竖直向上时,小球恰好在竖直平面内做匀速圆周运动,则重力与电场力一定平衡,即重力与电场力等大、反向,则:![]()
解得:![]()
(2)电场反向后,小球仍仍能在竖直平面内做完整的圆周运动,则当小球恰好能通过最高点时为临界状态,此时小球在最低点时速度最小
在最高点由重力和电场力的合力提供向心力,设最高点最小速度![]() ,根据牛顿第二定律得:
,根据牛顿第二定律得:![]()
小球由最低点运动到最高点的过程中,绳子拉力不做功,根据动能定理得:![]()
联立解得:![]()

练习册系列答案
相关题目