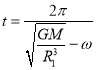题目内容
【题目】我们已经学过了关于两个质点之间万有引力的大小是：F=
．但是，在某些特殊情况下，非质点之间的万有引力计算及其应用的问题，我们可以利用下面两个已经被严格证明是正确的结论，而获得快速有效地解决：
a．若质点m放置在质量分布均匀的大球壳M（球壳的厚度也均匀）的空腔之内，那么m和M之间的万有引力总是为零．
b．若质点m放置在质量分布均匀的大球体M之外（r≥r0），那么它们之间的万有引力为：F=，式中的r为质点m到球心之间的距离; r0为大球体的半径．
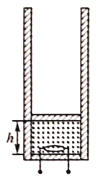
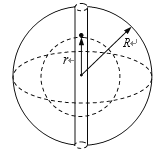
假设地球可视为一个质量分布均匀且密度为ρ的球体，通过地球的南北两极之间能够打通一个如图所示的真空小洞．若地球的半径为R，万有引力常数为G，把一个质量为m的小球从北极的洞口由静止状态释放后，小球能够在洞内运动．
（1）求：小球运动到距地心为0.5R处的加速度大小a；
（2）证明：小球在洞内做简谐运动；
（3）求：小球在运动过程中的最大速度vm．
【答案】（1）
（2）
做简谐运动（3）
【解析】
解：（1）根据题意可知，小球距离地心为r=0.5R处万有引力大小
又
由牛顿第二定律可知
三式联立可得：
（2）假设小球相对于球心的位移是x，则有：
又
两式联立可得：
考虑万有引力F的方向总是指向地心，即F的方向和小球相对于地心的位移x的方向总是方向相反的， 若令 ：
则有：
结论：小球在洞内做简谐振动．
（3） 由可知，从洞口到地心，小球的万有引力大小F是随着做功的距离线性减少的
所以
所以
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
