题目内容
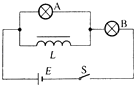
【题目】如图所示，正方形线圈abcd谢绕对称轴OO′在匀强磁场中匀速转动，转速为 
，已知ab=ad=20cm，匝数N=100，磁感应强度B=1T，图示位置线圈平面与磁感线平行．闭合回路中线圈的电阻r=4Ω，外电阻R=12Ω．求：
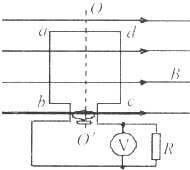
（1）线圈转动过程中感应电动势的最大值；
（2）从图示位置开始计时，写出感应电流的瞬时表达式；
（3）交流电压表的示数．
【答案】
（1）
解：根据法拉第电磁感应定律，则有最大值，为Em=NBL2ω
由角速度与转速的关系，ω=2πn
解得：Em=400V
（2）
解：感应电动势的瞬时值，e=Emcosωt
由闭合电路欧姆定律， 
解得：i=25cos100t（A）
（3）
解：最大值与有效值的关系， 
解得：U=150 
V
【解析】（1）根据法拉第电磁感应定律，及角速度与转速的关系，即可求解；（2）由感应电动势的瞬时值表达式，与闭合电路欧姆定律，即可求解；（3）由最大值与有效值的关系，与电压的分配与电阻的关系，即可求解．
【考点精析】解答此题的关键在于理解交流电的最大值与有效值的相关知识，掌握最大值:E m =NBSω，最大值E m （U m ，I m ）与线圈的形状，以及转动轴处于线圈平面内哪个位置无关.在考虑电容器的耐压值时，则应根据交流电的最大值；有效值:交流电的有效值是根据电流的热效应来规定的.即在同一时间内，跟某一交流电能使同一电阻产生相等热量的直流电的数值，叫做该交流电的有效值．
练习册系列答案
相关题目
