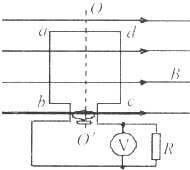
��Ŀ����
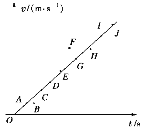
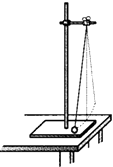
����Ŀ����ͼ��ʾ������m=50kg���˶�Ա������Ϊ�ʵ㣩���ںӰ���A�����һ����L=5.0m�IJ����쳤��������������һ��ϵ�ھ���ˮ���H=10.0m��O�㣬��ʱ��������ֱ����ļн�Ϊ��=37�㣬C����λ��O�����·�ˮ���ϵ�һ�㣬����C��x=5.0m����D����һֻ����Ȧ��O��A��C��D�������ͬһ��ֱ���ڣ����˶�Աץ�����˵㣬��̨����A���ش�ֱ������б������һ�����ٶ�Ծ�������ڵ�O�����·���B��ʱ�ɿ��֣�����ǡ�����ھ���Ȧ�ڣ���sin37��=0.6��cos37��=0.8��g=10m/s2����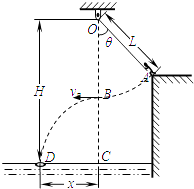
��1���˶�Ա����B��ʱ�ٶ�vB�Ĵ�С��
��2���˶�Ա����B��ʱ���ӵ�������С��
��3���˶�Ա��A��Ծ��ʱ�Ķ���Ek ��
���𰸡�
��1��
�⣺��B�˶���D�Ĺ��̣��˶�Ա��ƽ���˶�������
H��L= ![]()
�� t= ![]() =1s
=1s
��x=vBt�� vB= ![]() =5m/s
=5m/s
��2��
�⣺��B��ʱ����ţ�ٵڶ����ɵ�
F��mg=m ![]()
�� F=mg+m ![]() =750N
=750N
��3��
�⣺��ͼ�� hAB=L��1��cos�ȣ�=1m
���ݶ��ܶ�����
mghAB= ![]() ��Ek
��Ek
���Ek=125J
����������1���˶�Ա����B�����ƽ���˶�����֪����ĸ߶�h=H��L����h= ![]() ���ʱ�䣬��x=vBt����˶�Ա����B��ʱ�ٶ�vB�Ĵ�С����2���˶�Ա����B��ʱ�����������ӵ����������ṩ����������ţ�ٵڶ�����������ӵ�������С����3����A�˶���B�Ĺ����У�ֻ����������mgL��1��cos�ȣ������ݶ��ܶ�������˶�Ա��A��Ծ��ʱ�Ķ���Ek ��
���ʱ�䣬��x=vBt����˶�Ա����B��ʱ�ٶ�vB�Ĵ�С����2���˶�Ա����B��ʱ�����������ӵ����������ṩ����������ţ�ٵڶ�����������ӵ�������С����3����A�˶���B�Ĺ����У�ֻ����������mgL��1��cos�ȣ������ݶ��ܶ�������˶�Ա��A��Ծ��ʱ�Ķ���Ek ��
�����㾫�������ڱ��⿼����������Ͷ��ܶ������ۺ�Ӧ�ã���Ҫ�˽�����������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ����������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ��ܵó���ȷ�𰸣�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ���綯���г�����������Ҫ�Ľ�ͨ���ߣ�ijƷ�Ƶ綯���г����������£�
���ͣ� | ��ع�� |
20�磨����ֱ����508mm�� | 36V12Ah�����أ� |
����������40kg | �ת�٣�210r/min��ת/�֣� |
���γߴ磺 | ���ʱ�䣺2h��8h |
���������������ֱ������ʽ��� | �������ѹ/������36V/5A |
�����س����������ݴ������е��й����ݣ�����˵������ȷ���ǣ� ��
A.�ó��Ķ����ԼΪ4.32��102W
B.�ó��Ķʱ��ԼΪ20km/h
C.�ó�Լ����ʻ2.4Сʱ
D.�ó�һ�γ�����������ĵ���ԼΪ1.56��106J