题目内容
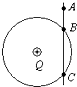 如图所示,光滑绝缘杆竖直放置,它与以正点电荷Q为圆心的某一圆周交于B、C两点,质量为m,带电量为-q的有孔小球从杆上A点无初速下滑,已知q<<Q,AB=h,BC=2h,小球滑到B点时速度大小为
如图所示,光滑绝缘杆竖直放置,它与以正点电荷Q为圆心的某一圆周交于B、C两点,质量为m,带电量为-q的有孔小球从杆上A点无初速下滑,已知q<<Q,AB=h,BC=2h,小球滑到B点时速度大小为| 3gh |
分析:小球由A到B重力和电场力做功,由动能定理求得小球从A点到B点的过程中电场力做的功;由于B、C两点在以正电荷Q为圆心的同一圆周上,电势相等,小球从B运动到C过程,电场力做功为零,根据动能定理研究小球从A运动到B的过程,求出电场力所做的功.
解答:解:小球由A到B重力和电场力做功,由动能定理,有:
mgh+W=
m
-0
解得:
W=
m
-mgh=
m×3gh-mgh=
小球从B运动到C过程,电场力做功为零,根据动能定理,有:
mg(2h)=
m
-
m
解得:
vC=
=
=
故答案为:
,
.
mgh+W=
| 1 |
| 2 |
| v | 2 B |
解得:
W=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| mgh |
| 2 |
小球从B运动到C过程,电场力做功为零,根据动能定理,有:
mg(2h)=
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 B |
解得:
vC=
|
| 3gh+4gh |
| 7gh |
故答案为:
| mgh |
| 2 |
| 7gh |
点评:本题关键将合运动沿水平和竖直方向正交分解,然后根据运动学公式列式分析.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 如图所示,光滑绝缘杆固定在水平位置上,使其两端分别带上等量同种正电荷Q1、Q2,杆上套着一带正电小球,整个装置处在一个匀强磁场中,磁感应强度方向垂直纸面向里,将靠近右端的小球从静止开始释放,在小球从右到左的运动过程中,下列说法正确的是( )
如图所示,光滑绝缘杆固定在水平位置上,使其两端分别带上等量同种正电荷Q1、Q2,杆上套着一带正电小球,整个装置处在一个匀强磁场中,磁感应强度方向垂直纸面向里,将靠近右端的小球从静止开始释放,在小球从右到左的运动过程中,下列说法正确的是( )| A、小球受到的洛伦兹力大小变化,但方向不变 | B、小球受到的洛伦兹力将不断增大 | C、小球的加速度将减小 | D、小球的电势能一直减小 |
 (2013?郑州二模)如图所示,光滑绝缘杆PQ放置在竖直平面内,PQ的形状与以初速度
(2013?郑州二模)如图所示,光滑绝缘杆PQ放置在竖直平面内,PQ的形状与以初速度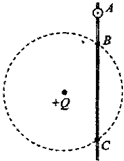 如图所示:光滑绝缘杆竖直放置,它与以正电荷Q为圆心的某一圆周交于B、C两点,质量为m,带电荷量为+q的有孔小球从杆上A点无初速下滑,已知q<Q,AB=h,小球滑到B点的速度大小为
如图所示:光滑绝缘杆竖直放置,它与以正电荷Q为圆心的某一圆周交于B、C两点,质量为m,带电荷量为+q的有孔小球从杆上A点无初速下滑,已知q<Q,AB=h,小球滑到B点的速度大小为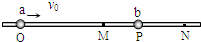 (2006?连云港一模)如图所示,光滑绝缘杆上套有两个完全相同、质量都是m的金属小球a、b,a带电量为q(q>0),b不带电.M点是ON的中点,且OM=MN=L,整个装置放在与杆平行的匀强电场中.开始时,b静止在杆上MN之间的某点P处,a从杆上O点以速度v0向右运动,到达M点时速度为3v0/4,再到P点与b球相碰并粘合在一起(碰撞时间极短),运动到N点时速度恰好为零.求:
(2006?连云港一模)如图所示,光滑绝缘杆上套有两个完全相同、质量都是m的金属小球a、b,a带电量为q(q>0),b不带电.M点是ON的中点,且OM=MN=L,整个装置放在与杆平行的匀强电场中.开始时,b静止在杆上MN之间的某点P处,a从杆上O点以速度v0向右运动,到达M点时速度为3v0/4,再到P点与b球相碰并粘合在一起(碰撞时间极短),运动到N点时速度恰好为零.求: