Question

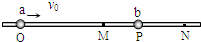（2006?连云港一模）如图所示，光滑绝缘杆上套有两个完全相同、质量都是m的金属小球a、b，a带电量为q（q＞0），b不带电．M点是ON的中点，且OM=MN=L，整个装置放在与杆平行的匀强电场中．开始时，b静止在杆上MN之间的某点P处，a从杆上O点以速度v₀向右运动，到达M点时速度为3v₀/4，再到P点与b球相碰并粘合在一起（碰撞时间极短），运动到N点时速度恰好为零．求：
（1）电场强度E的大小和方向；
（2）a、b两球碰撞中损失的机械能；
（3）a球碰撞b球前的速度v．

Answer 1

分析：（1）根据动能定理，即可确定电场强度的大小；由受力与运动分析，可确定电场强度的方向．
（2）根据能量守恒定律，从而可求出机械能损失．
（3）由动量守恒定律，即可求出动能的减小．

解答：解：（1）a球从O到M，
由动能定理，则有，W_OM=-qEL=

1

2

m(

3

4

v0)2-

1

2

m

v

2 0

解得：E=

7m v 2 0

32qL

  方向向左  
（2）设碰撞中损失的机械能为△E，对a、b球从O到N的全过程应用能的转化和守恒定律
-qE2L-△E=0-

1

2

mv02
则碰撞中损失的机械能为△E=

1

2

m

v

2 0

-

7

16

m

v

2 0

=

1

16

m

v

2 0

（3）设a与b碰撞前后的速度分别为v、v′，
则 动量守恒定律，mv=2mv’
减少的动能△E=

1

2

mv2-

1

2

2mv′2=

1

16

m

v

2 0

解得：v=

1

2

v 0
答：（1）电场强度：E=

7m v 2 0

32qL

和方向向左；
（2）a、b两球碰撞中损失的机械能

1

16

m

v

2 0

；
（3）a球碰撞b球前的速度

v0

2

．

点评：考查动能定理、能量守恒定律及动量守恒定律的应用与理解，突出动能定理的功的正负重要性，强调动量守恒定律的方向性．