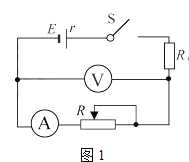
题目内容
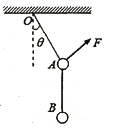
【题目】如图所示,倾角![]() =37°的足够长斜面上有一长为L、质量为2m的木板B,木板B上端有一质量为m的滑块A(视为质点),木板下端3L处有一质量为m的足够长木板C锁定。在斜面上,滑块A与木板B、C间的动摩擦因数均为μ1=0.25,木板C与斜面间无摩擦,木板B、C的厚度相同。现同时由静止释放A、B,在B与C碰撞前瞬间,解除对C的锁定,此时A恰好滑离B而滑上C,已知B、C碰撞为弹性碰撞,重力加速度为g,sin 37° = 0.6, cos 37°=0.8,求:
=37°的足够长斜面上有一长为L、质量为2m的木板B,木板B上端有一质量为m的滑块A(视为质点),木板下端3L处有一质量为m的足够长木板C锁定。在斜面上,滑块A与木板B、C间的动摩擦因数均为μ1=0.25,木板C与斜面间无摩擦,木板B、C的厚度相同。现同时由静止释放A、B,在B与C碰撞前瞬间,解除对C的锁定,此时A恰好滑离B而滑上C,已知B、C碰撞为弹性碰撞,重力加速度为g,sin 37° = 0.6, cos 37°=0.8,求:

(1)木板B与斜面间的动摩擦因数μ2;
(2)B、C发生碰撞后瞬间,木板C的速度大小vC;
(3)B、C发生碰撞后2s时,滑块A到木板C上端的距离x。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)0。
;(3)0。
【解析】
由题中“在B与C碰撞前瞬间,解除对C的锁定”可知,本题考查动量守恒和能量守恒定律,根据过程分析,运用动量守恒和能量守恒定律可分析本题。
(1)由题意可知,A、B同时滑下,且为匀变速运动,所以有
![]()
![]()
![]()
![]()
解得
![]()
(2)由第(1)问可知,当B与C碰撞时,B的速度为
![]()
B、C碰撞为弹性碰撞,故动量守恒,且机械能守恒,可得
![]()
![]()
联立解得
![]()
(3)BC发生弹性碰撞前,滑块A的速度
![]()
由于C碰撞后速度与A相同,且C与斜面无摩擦,故AC不发生相对滑动,以相同速度向下运动,故
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目