题目内容
物体在离水平地面20m高处作平抛运动,着地时的水平距离是4m。(g=10m/s2)求:
(1)初速度大小;
(2)着地速度的大小。(结果可用根号表示)
(1)初速度大小;
(2)着地速度的大小。(结果可用根号表示)

考点:
解析:平抛运动水平方向不受外力,做匀速直线运动,满足 ,竖直方向只受重力,初速度为0,分运动为自由落体,满足
,竖直方向只受重力,初速度为0,分运动为自由落体,满足 ,联立可得
,联立可得 。
。
着地速度为竖直分速度与水平分速度的合速度。水平分速度为 ,竖直方向,根据自由落体规律可知
,竖直方向,根据自由落体规律可知 ,据平行四边形定则
,据平行四边形定则 。
。
解析:平抛运动水平方向不受外力,做匀速直线运动,满足
 ,竖直方向只受重力,初速度为0,分运动为自由落体,满足
,竖直方向只受重力,初速度为0,分运动为自由落体,满足 ,联立可得
,联立可得 。
。着地速度为竖直分速度与水平分速度的合速度。水平分速度为
 ,竖直方向,根据自由落体规律可知
,竖直方向,根据自由落体规律可知 ,据平行四边形定则
,据平行四边形定则 。
。
练习册系列答案
相关题目
 向右抛出一小球,其落点与A的水平距离为
向右抛出一小球,其落点与A的水平距离为 ,若从A点以水平初速度
,若从A点以水平初速度 向右抛出同一小球,其落点与A的水平距离为
向右抛出同一小球,其落点与A的水平距离为 ,不计空气阻力,则
,不计空气阻力,则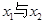 的比值可能为
的比值可能为