题目内容
 物体B放在物体A上,A、B的上下表面均与斜面平行(如图).当两者以相同的初速度靠惯性沿光滑固定斜面C向上做匀减速运动时( )
物体B放在物体A上,A、B的上下表面均与斜面平行(如图).当两者以相同的初速度靠惯性沿光滑固定斜面C向上做匀减速运动时( )分析:先对A、B整体受力分析,求出加速度;再隔离出物体B,受力分析,根据牛顿第二定律列方程求未知力.
解答:解:先对A、B整体受力分析,受重力和支持力,合力沿斜面向下,根据牛顿第二定律,有
(m1+m2)gsinθ=(m1+m2)a (θ为斜面的倾角)
解得
a=gsinθ ①
再隔离出物体B受力分析,受重力、支持力,假设有沿斜面向上的静摩擦力f,如图
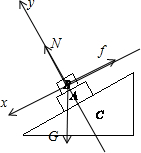
根据牛顿第二定律,有
m2gsinθ-f=ma ②
由①②两式可解得
f=0
故A对B的摩擦力为零;
故选C.
(m1+m2)gsinθ=(m1+m2)a (θ为斜面的倾角)
解得
a=gsinθ ①
再隔离出物体B受力分析,受重力、支持力,假设有沿斜面向上的静摩擦力f,如图

根据牛顿第二定律,有
m2gsinθ-f=ma ②
由①②两式可解得
f=0
故A对B的摩擦力为零;
故选C.
点评:本题关键先用整体法求出整体的加速度,然后隔离出物体B,假设摩擦力为f,对其受力分析后根据牛顿第二定律求解出摩擦力.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 物体B放在物体A上,A、B的上下表面均与斜面平行(如图),当两者以相同的初速度靠惯性沿光滑斜面C向上做匀减速运动时,斜面体C静止于地面,则( )
物体B放在物体A上,A、B的上下表面均与斜面平行(如图),当两者以相同的初速度靠惯性沿光滑斜面C向上做匀减速运动时,斜面体C静止于地面,则( ) 物体B放在物体A上,A、B的上下表面均与斜面平行,如图所示,当两者以相同的初速度靠惯性沿粗糙固定斜面C向上做匀减速运动时( )
物体B放在物体A上,A、B的上下表面均与斜面平行,如图所示,当两者以相同的初速度靠惯性沿粗糙固定斜面C向上做匀减速运动时( ) 物体B放在物体A上,A、B的上下表面均与斜面平行,物体F放在物体E上,E、F接触面水平,当A与B相对静止,E与F相对静止从光滑斜面上滑下时( )
物体B放在物体A上,A、B的上下表面均与斜面平行,物体F放在物体E上,E、F接触面水平,当A与B相对静止,E与F相对静止从光滑斜面上滑下时( ) 物体B放在物体A上,A、B的上下表面均与斜面平行,如图所示.两物体恰能沿固定斜面向下做匀速运动( )
物体B放在物体A上,A、B的上下表面均与斜面平行,如图所示.两物体恰能沿固定斜面向下做匀速运动( )