题目内容
9.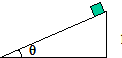 物体沿高为h、倾角为θ的斜面由静止下滑:
物体沿高为h、倾角为θ的斜面由静止下滑:(1)若斜面光滑,物块到达底端的速度大小$\sqrt{2gh}$ m/s
(2)若斜面与物块间的动摩擦因数为μ,求物块到达斜面底端的速度大小$\sqrt{2gh(1-μcotθ)}$ m/s.
分析 (1)若斜面光滑,只有重力做功,根据动能定理或机械能守恒定律求物块到达底端的速度大小.
(2)若斜面与物块间的动摩擦因数为μ,重力和摩擦力做功,由动能定理求解.
解答 解:(1)若斜面光滑,根据机械能守恒定律得
mgh=$\frac{1}{2}m{v}^{2}$
则得 v=$\sqrt{2gh}$
(2)若斜面与物块间的动摩擦因数为μ,重力和摩擦力做功,由动能定理得
mgh-μmgcosθ$•\frac{h}{sinθ}$=$\frac{1}{2}mv{′}^{2}$
解得 v′=$\sqrt{2gh(1-μcotθ)}$
故答案为:(1)$\sqrt{2gh}$.(2)$\sqrt{2gh(1-μcotθ)}$.
点评 本题要注意机械能守恒定律和动能定理应用条件的不同,机械能守恒是有条件的,动能定理没有条件,所以能用机械能守恒定律求的,一定能用动能定理,但能用动能定理的,不一定能用机械能守恒定律.

练习册系列答案
相关题目
19.某质点在xoy平面上运动,其在x轴方向和y轴方向上的v-t图象分别如图甲和图乙所示.则下列判断正确的是( )


| A. | 该质点做匀变速直线运动 | |
| B. | 该质点有恒定的加速度,大小为2.5 m/s2 | |
| C. | 该质点的初速度为7 m/s | |
| D. | 前2s内质点的位移为4221 m |
17.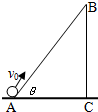 如图所示,长为L、倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q质量为m的小球,以初速度v0从斜面底端A点开始沿斜面上滑,当达到斜面顶端B点时,速度仍为vo,则下列说法正确的是( )
如图所示,长为L、倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q质量为m的小球,以初速度v0从斜面底端A点开始沿斜面上滑,当达到斜面顶端B点时,速度仍为vo,则下列说法正确的是( )
 如图所示,长为L、倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q质量为m的小球,以初速度v0从斜面底端A点开始沿斜面上滑,当达到斜面顶端B点时,速度仍为vo,则下列说法正确的是( )
如图所示,长为L、倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q质量为m的小球,以初速度v0从斜面底端A点开始沿斜面上滑,当达到斜面顶端B点时,速度仍为vo,则下列说法正确的是( )| A. | A、B两点间的电势差一定等于$\frac{mgLsinθ}{q}$ | |
| B. | 小球在B点的电势能一定大于在A点的电势能 | |
| C. | 若该电场是匀强电场,则其电场强度的最大值一定为$\frac{mg}{q}$ | |
| D. | 若该电场是由斜面上方某位置的点电荷产生的,则该点电荷一定为负点电荷,且处于斜面中点的正上方 |
4.两颗人造卫星A、B绕地球做圆周运动,周期之比TA:TB=1:8,则轨道半径之比和运动的速率分别为( )
| A. | RA:RB=1:4 VA:VB=4:1 | B. | RA:RB=1:2 VA:VB=2:1 | ||
| C. | RA:RB=1:4 VA:VB=2:1 | D. | RA:RB=1:2 VA:VB=4:1 |
1.关于重力和重心,下面说法正确的是( )
| A. | 质量为1kg的物体所受的重力一定等于9.8N | |
| B. | 物体所受重力的大小跟物体的运动情况有关 | |
| C. | 物体的重心由物体的几何形状和质量分布情况决定 | |
| D. | 物体的重心跟物体如何放置有关 |
18.关于力、运动状态及惯性的说法,下列正确的是( )
| A. | 牛顿最早指出力不是维持物体运动的原因 | |
| B. | 笛卡尔对牛顿第一定律的建立做出了贡献 | |
| C. | 一个运动的物体,如果不再受力了,它总会逐渐停下来,这说明,静止状态才是物体长时间不受力时的“自然状态 | |
| D. | 车速越大,刹车后滑行的路程越长,所以惯性越大 |
 有一种地铁,车辆进站时要上坡,出站时要下坡.如图所示,如果站台高2m,车辆到达A处时速度是25.2km/h,以后关闭发动机,不考虑阻力,车辆到达B处时速度是10.8km/h.
有一种地铁,车辆进站时要上坡,出站时要下坡.如图所示,如果站台高2m,车辆到达A处时速度是25.2km/h,以后关闭发动机,不考虑阻力,车辆到达B处时速度是10.8km/h.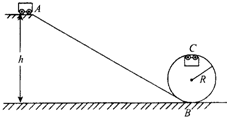 如图是一个设计“过山车”的试验装置的原理示意图.斜面AB与竖直面内的圆形轨道在B点平滑连接.斜面AB和圆形轨道都是光滑的.圆形轨道半径为R.一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,A点距水平面的高度h=2.5R,已知重力加速度为g. 求:
如图是一个设计“过山车”的试验装置的原理示意图.斜面AB与竖直面内的圆形轨道在B点平滑连接.斜面AB和圆形轨道都是光滑的.圆形轨道半径为R.一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,A点距水平面的高度h=2.5R,已知重力加速度为g. 求: