题目内容
4.两颗人造卫星A、B绕地球做圆周运动,周期之比TA:TB=1:8,则轨道半径之比和运动的速率分别为( )| A. | RA:RB=1:4 VA:VB=4:1 | B. | RA:RB=1:2 VA:VB=2:1 | ||
| C. | RA:RB=1:4 VA:VB=2:1 | D. | RA:RB=1:2 VA:VB=4:1 |
分析 根据人造卫星的万有引力等于向心力,列式求出线速度、周期的表达式进行讨论即可.
解答 解:根据万有引力提供向心力为:
$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}=m\frac{{v}^{2}}{r}$,
解得:r=$\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}$,v=$\sqrt{\frac{GM}{r}}$
因为TA:TB=1:8
所以:RA:RB=1:4
所以:VA:VB=2:1
故选:C
点评 能根据万有引力提供圆周运动向心力正确得到线速度和周期与轨道半径的关系是解决本题的关键.

练习册系列答案
相关题目
14.我国某城市某交通路口绿灯即将结束时会持续闪烁3s,而后才会变成黄灯,再在3秒黄灯提示后再转为红灯.2013年1月1日实施新的交通规定:黄灯亮时车头已经越过停车线的车辆可以继续前行,车头未越过停车线的若继续前行则视为闯黄灯,属于交通违章行为.(本题中的刹车过程均视为匀减速直线运动)( )
| A. | 若某车在绿灯开始闪烁时刹车,要使车在绿灯闪烁的时间内停下来且刹车距离不得大于27 m,该车刹车前的行驶速度不能超过12m/s | |
| B. | 若某车在绿灯开始闪烁时刹车,要使车在绿灯闪烁的时间内停下来且刹车距离不得大于27 m,该车刹车前的行驶速度不能超16m/s | |
| C. | 若某车正以v0=18m/s的速度驶向路口当驾驶员看到绿灯开始闪烁时,经0.5秒短暂考虑后开始刹车,该车在红灯刚亮时恰停在停车线以内.则此车在绿灯开始闪烁时到停下来的距离为60m | |
| D. | 若某车正以v0=18m/s的速度驶向路口当驾驶员看到绿灯开始闪烁时,经0.5秒短暂考虑后开始刹车,该车在红灯刚亮时恰停在停车线以内.则此车在绿灯开始闪烁时到停下来的距离为58.5m |
16.${\;}_{90}^{232}$Th(钍)经过一系列α衰变和β衰变,变成${\;}_{82}^{208}$Pb(铅).以下说法正确的是( )
| A. | 铅核比钍核少8个质子 | B. | 铅核比钍核少16个中子 | ||
| C. | 共经过4次α衰变和6次β衰变 | D. | 共经过6次α衰变和4次β衰变 |
8.关于速度,速度改变量,加速度,下列说法正确的是( )
| A. | 物体运动的速度改变量很大,它的加速度一定很大 | |
| B. | 速度很大的物体,其加速度可以很小,可以为零 | |
| C. | 某时刻物体的速度为零,其加速度一定为零 | |
| D. | 加速度很大时,运动物体的速度一定很大 |
 如图所示,足够长的传送带水平放置,以速度v=4m/s向右匀速转动,传送带上表面离地面的高度h=0.45m,一质量为m=1kg的物块,以速度v0=6m/s向左滑上传送带,与传送带之间的动摩擦因数为μ=0.2,g取10m/s2,求:
如图所示,足够长的传送带水平放置,以速度v=4m/s向右匀速转动,传送带上表面离地面的高度h=0.45m,一质量为m=1kg的物块,以速度v0=6m/s向左滑上传送带,与传送带之间的动摩擦因数为μ=0.2,g取10m/s2,求: 两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态.在它们左边有一垂直轨道的固定档板P,右边有一小球C沿轨道以速度v0射向B球,如图所示,C与B发生碰撞并立即结成一个整体D.在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变.然后,A球与档板P发生碰撞,碰后A、D静止不动,A与P接触而不粘连.过一段时间,突然解除锁定(锁定及解除锁定均无机械能损失),已知A、B、C三球的质量均为m.
两个小球A和B用轻质弹簧相连,在光滑的水平直轨道上处于静止状态.在它们左边有一垂直轨道的固定档板P,右边有一小球C沿轨道以速度v0射向B球,如图所示,C与B发生碰撞并立即结成一个整体D.在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变.然后,A球与档板P发生碰撞,碰后A、D静止不动,A与P接触而不粘连.过一段时间,突然解除锁定(锁定及解除锁定均无机械能损失),已知A、B、C三球的质量均为m. 如图所示,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开轻质接触式开关S,同时被电磁铁吸住的小球B自行脱落,改变距地面的高度H再重复几次.两球体积较小,密度较大.请回答下列两个问题:
如图所示,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开轻质接触式开关S,同时被电磁铁吸住的小球B自行脱落,改变距地面的高度H再重复几次.两球体积较小,密度较大.请回答下列两个问题: 物体沿高为h、倾角为θ的斜面由静止下滑:
物体沿高为h、倾角为θ的斜面由静止下滑: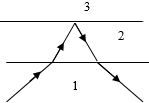 一束光从介质1射向介质2,再射向介质3的光路如图所示,则三种介质的折射率n1、n2、n3的大小关系是n1<n2<n3,在三种介质中的传播速度为v1、v2、v3的大小关系是v1>v2>v3.
一束光从介质1射向介质2,再射向介质3的光路如图所示,则三种介质的折射率n1、n2、n3的大小关系是n1<n2<n3,在三种介质中的传播速度为v1、v2、v3的大小关系是v1>v2>v3.