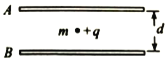��Ŀ����
����Ŀ����ͼ��ʾ����һ����Դ����������ABO�������ٶȴ�С��ͬ�����ӣ�����������Ϊm���������q��A��B�Dz��ӵ�ѹ�Ҵ��ڹر�״̬���������ţ����ź���һ��ƽ�м��壬��������Ϊd���ϼ���ӵأ��¼���ĵ�����ʱ��仯��ϵ��ͼ��b����ʾ��O����һ�����ߴ�ֱ�Ľ���������OΪԭ�㣬��ֱ������ABO����Ϊy��������ͬ�ٶȵ����Ӵ��ڽ������϶�Ӧ��ͬ�����꣬����ߴ��ͼ��a��������l��t��Ϊ��֪����֪ ![]() ����������������
����������������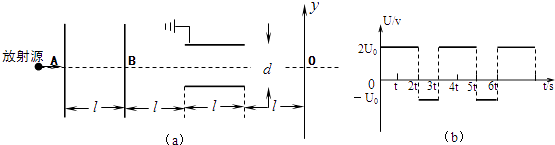
��1��ijʱ��A��Bͬʱ�����Ҳ��ٹرգ���һ���ٶ�Ϊ ![]() ������ǡ�ڴ�ʱͨ��A���ţ��Է��ſ���ʱ����Ϊͼ��b���еļ�ʱ��㣬��������Ӵ���y���ϵ�����λ�ã���d��ʾ����
������ǡ�ڴ�ʱͨ��A���ţ��Է��ſ���ʱ����Ϊͼ��b���еļ�ʱ��㣬��������Ӵ���y���ϵ�����λ�ã���d��ʾ����
��2��ijʱ��A������ ![]() ��A�رգ��ֹ�
��A�رգ��ֹ� ![]() ��B�������ٹ�
��B�������ٹ� ![]() ��BҲ�رգ����ܴ�������B�����ӵ�����ٶȺ���С�ٶȣ�
��BҲ�رգ����ܴ�������B�����ӵ�����ٶȺ���С�ٶȣ�
��3���ڵڶ����У�����B����ʱ����Ϊͼ��b���еļ�ʱ��㣬����������������Ӵ������ϵ�y���꣨��d��ʾ����
���𰸡�
��1���⣺�辭ʱ��t0����ƫת�糡���У� ![]() ��
��
����tʱ�̽���ƫת�糡���ڵ糡�е��˶�ʱ��Ϊ�� ![]() ��
��
ƫת�糡�еļ��ٶ�Ϊ�� ![]()
�ڳ��е�ƫת����Ϊ�� ![]() ��
��
��ã� ![]() ��
��
�ڵ糡�е�ƫת�ǣ� ![]() ��
��
�ӳ�ƫת�糡��������ƫת���룺
y2=ltan�ȣ�y=y1+y2
��ã� ![]() ��
��
�𣺴����Ӵ���y���ϵ�����λ��Ϊ ![]() d��
d��
��2���⣺�ܴ�������B�����ʱ��Ϊ ![]() ��
��
��Ӧ����ٶȣ� ![]() ��
��
�ܴ�������B���ʱ��Ϊ ![]() ��
��
��Ӧ��С�ٶȣ� ![]() ��
��
���ܴ�������B�����ӵ�����ٶ�Ϊ ![]() ����С�ٶ�Ϊ
����С�ٶ�Ϊ ![]() ��
��
��3���⣺�ٶ��������ӽ���0ʱ�̳�����B�� ![]() ʱ�̽���ƫת�糡
ʱ�̽���ƫת�糡
����ƫת������ڣ�1������ͬ������y���ϵ�����Ϊ ![]() ��
��
�ٶ���С�����ӽ��� ![]() ʱ�̳�����B��2tʱ�̽���ƫת�糡��
ʱ�̳�����B��2tʱ�̽���ƫת�糡��
������ƫתʱ��Ϊt�����У� ![]() ��
��
![]() ��
��
������ƫת�����٣� ![]() ���糡ʱǡ���ٶ�ˮƽ��
���糡ʱǡ���ٶ�ˮƽ�� ![]() ����
����
![]() ��
�� ![]() ��
��
����������ֱ�Ϊ���� ![]() ����
����
�������������Ӵ������ϵ�y����Ϊ�� ![]() d����
d���� ![]() d����
d����
����������1�����⣬A��B�䲻�ӵ�ѹ��������AB��������ֱ���˶������ӽ���ƽ�м��������ƽ���˶��������˶����������ֽ⣬��ˮƽ����������˶������������ͨ���糡��ʱ�䣬��ţ�ٵڶ����ɺ��˶�ѧ��ʽ����������ڵ糡�е�ƫת�����ƫת�Ƕȣ������뿪�糡��������ֱ���˶�������ѧ֪ʶ�������Ӵ���y���ϵ�����λ��y����2���ܴ�������B�����ʱ��Ϊ ![]() ����Ӧ����ٶ�vmax=
����Ӧ����ٶ�vmax= ![]() ���ܴ�������B���ʱ��Ϊ
���ܴ�������B���ʱ��Ϊ ![]() t����Ӧ��С�ٶ� vmin=
t����Ӧ��С�ٶ� vmin= ![]() ����3�����õ�1�����Ƶķ�������������Ӵ������ϵ�y���꣮
����3�����õ�1�����Ƶķ�������������Ӵ������ϵ�y���꣮