题目内容
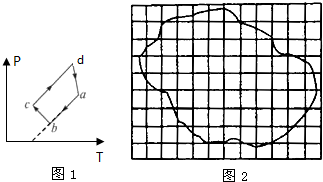
 (1)一定质量的理想气体,从状态A变化到状态B,其压强p和温度T的关系如图所示,
(1)一定质量的理想气体,从状态A变化到状态B,其压强p和温度T的关系如图所示,则理想气体的分子平均动能
增大
增大
(填“增大”或“减小”).若此过程中气体的内能变化1.2×105J,气体对外做功1.0×105,则气体
吸
吸
热(填“吸”或“放”)2.2×105
2.2×105
J.(2)体积为V的纯油酸在水面上完全散开的面积为S,则油酸分子直径为
| V |
| S |
| V |
| S |
若油酸的摩尔质量为M,密度为p,则阿伏伽德罗常数NA=
| 6MS3 |
| πρV3 |
| 6MS3 |
| πρV3 |
积V与直径D的关系为V=
| 1 |
| 6 |
分析:根据气体状态方程和已知的变化量去判断其它的物理量.对于一定质量的理想气体,温度升高,那么气体的平均动能和内能都增加.根据热力学第一定律判断气体吸热还是放热.
油酸溶液滴在水面上扩散后形成的油酸油膜最大面积时,形成单分子油膜,油膜的厚度等于分子直径.由油酸的体积与面积之比求出分子直径.把分子看成立文体形,阿伏加德罗常量为NA等于摩尔体积与分子体积之比.
油酸溶液滴在水面上扩散后形成的油酸油膜最大面积时,形成单分子油膜,油膜的厚度等于分子直径.由油酸的体积与面积之比求出分子直径.把分子看成立文体形,阿伏加德罗常量为NA等于摩尔体积与分子体积之比.
解答:解:(1)由图象知气体的温度增加,分子的平均动能增大,内能升高,由热力学第一定律公式:△U=Q+W,知Q=△U-W=1.2×105+1.0×105=2.2×105J,即吸收热量.
(2)体积为V的纯油酸在水面上完全散开的面积为S,则油酸分子直径为d=
,把油酸分子看成立球体,则有:NA?
π(
)3=
代入解得:NA=
故答案为:增大,吸,2.2×105,
,
(2)体积为V的纯油酸在水面上完全散开的面积为S,则油酸分子直径为d=
| V |
| S |
| 4 |
| 3 |
| d |
| 2 |
| M |
| ρ |
代入解得:NA=
| 6MS3 |
| πρV3 |
故答案为:增大,吸,2.2×105,
| V |
| S |
| 6MS3 |
| πρV3 |
点评:对于气体状态图象,根据气态方程分析状态变化过程,要掌握一定质量的理想气体的内能只跟温度有关.对单分子油膜法测定分子直径原理的理解和应用,建立模型是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 (2011?鹰潭一模)(1)一定质量的理想气体封闭在气缸内,当用活塞压缩气体时,一定增大的物理量为
(2011?鹰潭一模)(1)一定质量的理想气体封闭在气缸内,当用活塞压缩气体时,一定增大的物理量为